Question Number 157781 by amin96 last updated on 27/Oct/21
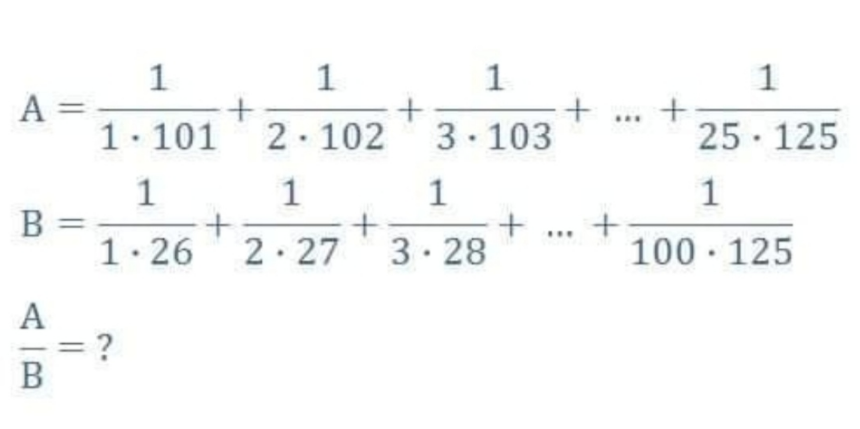
Answered by mr W last updated on 27/Oct/21
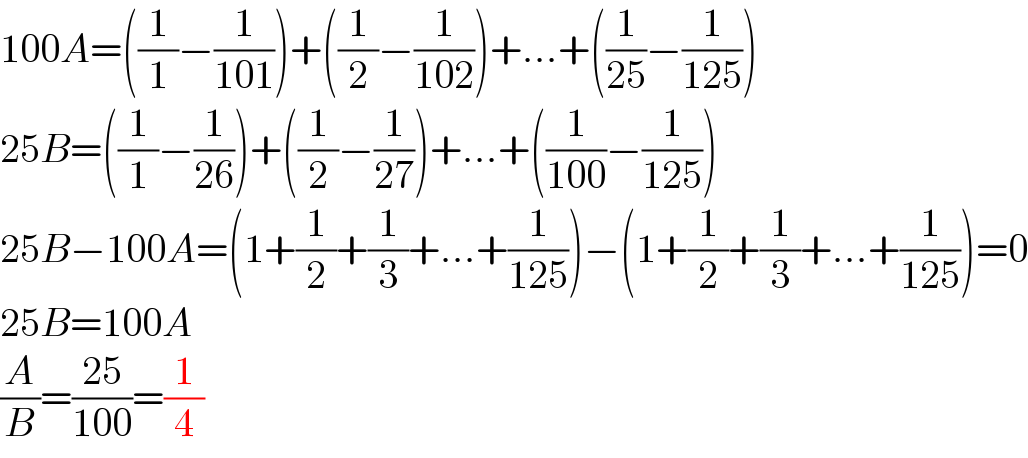
$$\mathrm{100}{A}=\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{101}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{102}}\right)+…+\left(\frac{\mathrm{1}}{\mathrm{25}}−\frac{\mathrm{1}}{\mathrm{125}}\right) \\ $$$$\mathrm{25}{B}=\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{26}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{27}}\right)+…+\left(\frac{\mathrm{1}}{\mathrm{100}}−\frac{\mathrm{1}}{\mathrm{125}}\right) \\ $$$$\mathrm{25}{B}−\mathrm{100}{A}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{125}}\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{125}}\right)=\mathrm{0} \\ $$$$\mathrm{25}{B}=\mathrm{100}{A} \\ $$$$\frac{{A}}{{B}}=\frac{\mathrm{25}}{\mathrm{100}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
