Question Number 157797 by akolade last updated on 28/Oct/21
Answered by MJS_new last updated on 28/Oct/21

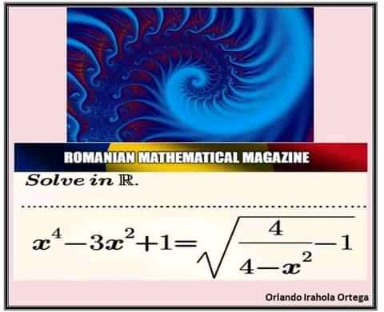
$${x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}=\sqrt{\frac{\mathrm{4}}{\mathrm{4}−{x}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${x}^{\mathrm{10}} −\mathrm{10}{x}^{\mathrm{8}} +\mathrm{35}{x}^{\mathrm{6}} −\mathrm{50}{x}^{\mathrm{4}} +\mathrm{26}{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}\right)\left({x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}\vee{x}^{\mathrm{2}} =\mathrm{2}\pm\sqrt{\mathrm{3}}\vee{x}^{\mathrm{2}} =\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$$\mathrm{testing}\:\mathrm{all}\:\mathrm{solutions}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}}\vee{x}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{2}}\vee{x}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$${x}=\pm\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\vee{x}=\pm\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\vee{x}=\pm\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
