Question Number 15782 by mrW1 last updated on 13/Jun/17
Commented by mrW1 last updated on 13/Jun/17

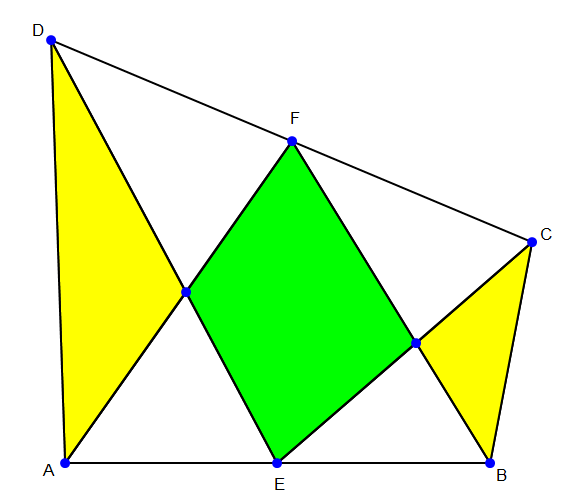
$$\mathrm{E}\:\mathrm{and}\:\mathrm{F}\:\mathrm{are}\:\mathrm{midpoint}\:\mathrm{of}\:\mathrm{AB}\:\mathrm{and}\:\mathrm{CD}.\: \\ $$$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{area}\:\mathrm{yellow}=\mathrm{area}\:\mathrm{green} \\ $$
Answered by ajfour last updated on 14/Jun/17
Commented by ajfour last updated on 14/Jun/17
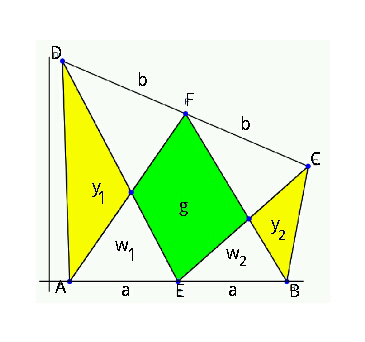
![area w_1 +w_2 +g = (1/2)(2a)h_F ...(i) w_1 +y_1 = (1/2)ah_D ...(ii) w_2 +y_2 = (1/2)ah_C ...(iii) (i)−(ii)−(iii) gives g−(y_1 +y_2 )=(a/2)[2h_F −(h_D +h_C )] F is mid-point of CD, so h_F =((h_D +h_C )/2) ⇒ 2h_F −h_D −h_C =0 means g−(y_1 +y_2 )=0 area_(green) = area_(yellow) .](https://www.tinkutara.com/question/Q15822.png)
$${area}\:\:\:\:{w}_{\mathrm{1}} +{w}_{\mathrm{2}} +{g}\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}\right){h}_{{F}} \:\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{w}_{\mathrm{1}} \:+{y}_{\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}{ah}_{{D}} \:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{w}_{\mathrm{2}} +{y}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}}{ah}_{{C}} \:\:\:\:\:\:…\left({iii}\right) \\ $$$$\:\left({i}\right)−\left({ii}\right)−\left({iii}\right)\:\:{gives} \\ $$$$\:\:\:\:{g}−\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)=\frac{{a}}{\mathrm{2}}\left[\mathrm{2}{h}_{{F}} −\left({h}_{{D}} +{h}_{{C}} \right)\right] \\ $$$${F}\:{is}\:{mid}-{point}\:{of}\:{CD},\:{so} \\ $$$$\:{h}_{{F}} =\frac{{h}_{{D}} +{h}_{{C}} }{\mathrm{2}}\:\:\:\Rightarrow\:\mathrm{2}{h}_{{F}} −{h}_{{D}} −{h}_{{C}} =\mathrm{0} \\ $$$${means}\:\:\:\:{g}−\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{area}_{{green}} =\:{area}_{{yellow}} \:. \\ $$
Commented by mrW1 last updated on 14/Jun/17

$$\mathrm{very}\:\mathbb{NICE}\:\mathrm{sir}! \\ $$
