Question Number 157822 by MathSh last updated on 28/Oct/21
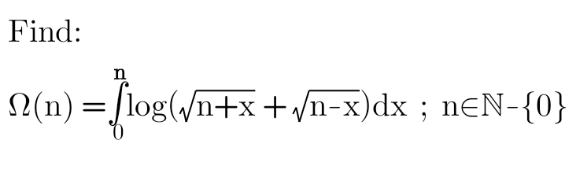
Commented by HongKing last updated on 28/Oct/21
![let x=ncos2α ⇒ dx=-2nsin2α∙dα Ω(n)=n((1/2)log(2n)+Υ) Υ=∫_( (𝛑/4) ) ^( 0) log(cosα+sinα)(d/dα)(cos2α)dα=((π-2)/4) thus, Ω(n)=n((1/2)log(2n)+((π-2)/4))=(n/4)[2log(2n)+π-2]](https://www.tinkutara.com/question/Q157837.png)
$$\mathrm{let}\:\mathrm{x}=\mathrm{ncos2}\alpha\:\Rightarrow\:\mathrm{dx}=-\mathrm{2nsin2}\alpha\centerdot\mathrm{d}\alpha \\ $$$$\Omega\left(\mathrm{n}\right)=\mathrm{n}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2n}\right)+\Upsilon\right) \\ $$$$\Upsilon=\underset{\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\:} {\overset{\:\mathrm{0}} {\int}}\mathrm{log}\left(\mathrm{cos}\alpha+\mathrm{sin}\alpha\right)\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(\mathrm{cos2}\alpha\right)\mathrm{d}\alpha=\frac{\pi-\mathrm{2}}{\mathrm{4}} \\ $$$$\mathrm{thus}, \\ $$$$\Omega\left(\mathrm{n}\right)=\mathrm{n}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2n}\right)+\frac{\pi-\mathrm{2}}{\mathrm{4}}\right)=\frac{\mathrm{n}}{\mathrm{4}}\left[\mathrm{2log}\left(\mathrm{2n}\right)+\pi-\mathrm{2}\right] \\ $$
