Question Number 157826 by cortano last updated on 28/Oct/21
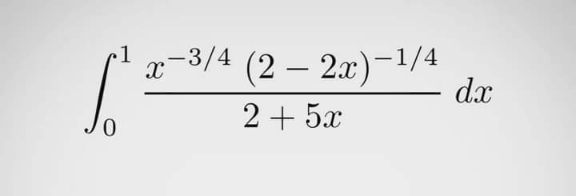
Answered by MJS_new last updated on 29/Oct/21
![∫_0 ^1 (dx/((2+5x)((2x^3 (1−x)))^(1/4) ))= [t=(((7x)/(2(1−x))))^(1/4) → dx=4(((2x^3 (1−x)^5 )/7))^(1/4) dt] =(2/7^(1/4) )∫_0 ^∞ (dt/(t^4 +1))= =(1/(2^(3/2) 7^(1/4) ))[ln ((t^2 +(√2)t+1)/(t^2 −(√2)t+1)) +2(arctan ((√2)t+1) +arctan ((√2)t−1))]_0 ^∞ = =(π/(2^(1/2) 7^(1/4) )) (=(π/( ((28))^(1/4) )))](https://www.tinkutara.com/question/Q157927.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\left(\mathrm{2}+\mathrm{5}{x}\right)\sqrt[{\mathrm{4}}]{\mathrm{2}{x}^{\mathrm{3}} \left(\mathrm{1}−{x}\right)}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{7}{x}}{\mathrm{2}\left(\mathrm{1}−{x}\right)}}\:\rightarrow\:{dx}=\mathrm{4}\sqrt[{\mathrm{4}}]{\frac{\mathrm{2}{x}^{\mathrm{3}} \left(\mathrm{1}−{x}\right)^{\mathrm{5}} }{\mathrm{7}}}{dt}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{7}^{\mathrm{1}/\mathrm{4}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}/\mathrm{2}} \mathrm{7}^{\mathrm{1}/\mathrm{4}} }\left[\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}\:+\mathrm{2}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)\right)\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\pi}{\mathrm{2}^{\mathrm{1}/\mathrm{2}} \mathrm{7}^{\mathrm{1}/\mathrm{4}} }\:\left(=\frac{\pi}{\:\sqrt[{\mathrm{4}}]{\mathrm{28}}}\right) \\ $$
Commented by cortano last updated on 30/Oct/21

$${great} \\ $$
