Question Number 157851 by emanuelMcCarthy last updated on 28/Oct/21

Commented by otchereabdullai@gmail.com last updated on 29/Oct/21
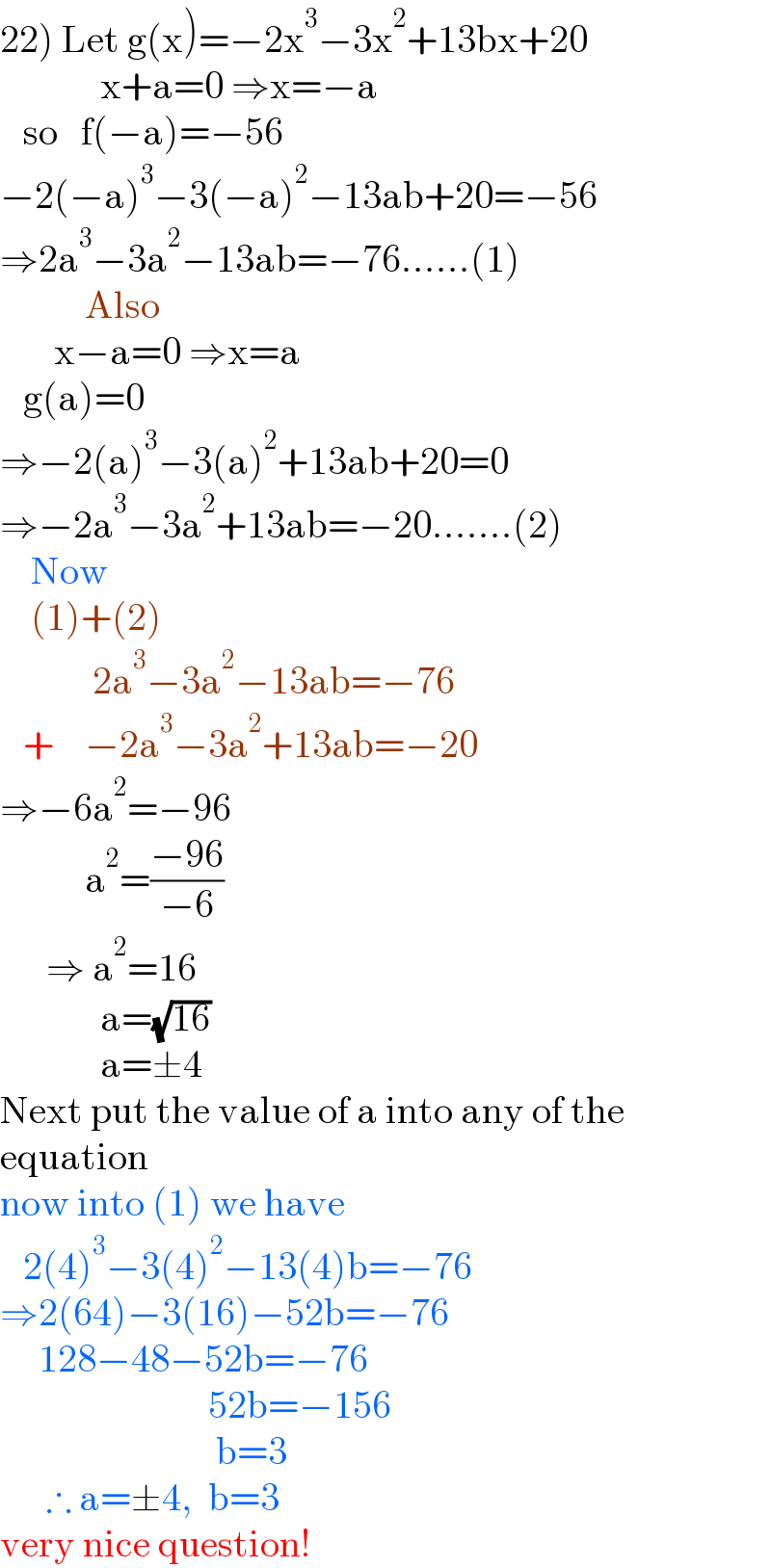
$$\left.\mathrm{22}\right)\:\mathrm{Let}\:\mathrm{g}\left(\mathrm{x}\right)=−\mathrm{2x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{13bx}+\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{x}=−\mathrm{a} \\ $$$$\:\:\:\mathrm{so}\:\:\:\mathrm{f}\left(−\mathrm{a}\right)=−\mathrm{56} \\ $$$$−\mathrm{2}\left(−\mathrm{a}\right)^{\mathrm{3}} −\mathrm{3}\left(−\mathrm{a}\right)^{\mathrm{2}} −\mathrm{13ab}+\mathrm{20}=−\mathrm{56} \\ $$$$\Rightarrow\mathrm{2a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} −\mathrm{13ab}=−\mathrm{76}……\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{Also} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}−\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{x}=\mathrm{a} \\ $$$$\:\:\:\mathrm{g}\left(\mathrm{a}\right)=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{2}\left(\mathrm{a}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{a}\right)^{\mathrm{2}} +\mathrm{13ab}+\mathrm{20}=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{2a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} +\mathrm{13ab}=−\mathrm{20}…….\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\mathrm{Now} \\ $$$$\:\:\:\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} −\mathrm{13ab}=−\mathrm{76} \\ $$$$\:\:\:+\:\:\:\:−\mathrm{2a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} +\mathrm{13ab}=−\mathrm{20} \\ $$$$\Rightarrow−\mathrm{6a}^{\mathrm{2}} =−\mathrm{96} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} =\frac{−\mathrm{96}}{−\mathrm{6}} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\mathrm{a}^{\mathrm{2}} =\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}=\sqrt{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}=\pm\mathrm{4} \\ $$$$\mathrm{Next}\:\mathrm{put}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}\:\mathrm{into}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation} \\ $$$$\mathrm{now}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\:\:\mathrm{2}\left(\mathrm{4}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{4}\right)^{\mathrm{2}} −\mathrm{13}\left(\mathrm{4}\right)\mathrm{b}=−\mathrm{76} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{64}\right)−\mathrm{3}\left(\mathrm{16}\right)−\mathrm{52b}=−\mathrm{76} \\ $$$$\:\:\:\:\:\mathrm{128}−\mathrm{48}−\mathrm{52b}=−\mathrm{76} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{52b}=−\mathrm{156} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\therefore\:\mathrm{a}=\pm\mathrm{4},\:\:\mathrm{b}=\mathrm{3} \\ $$$$\mathrm{very}\:\mathrm{nice}\:\mathrm{question}! \\ $$
Commented by Tinku Tara last updated on 29/Oct/21

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{rotate}\:\mathrm{image}\:\mathrm{in}\:\mathrm{correct} \\ $$$$\mathrm{orientation}\:\mathrm{before}\:\mathrm{uploading} \\ $$
Answered by otchereabdullai@gmail.com last updated on 29/Oct/21
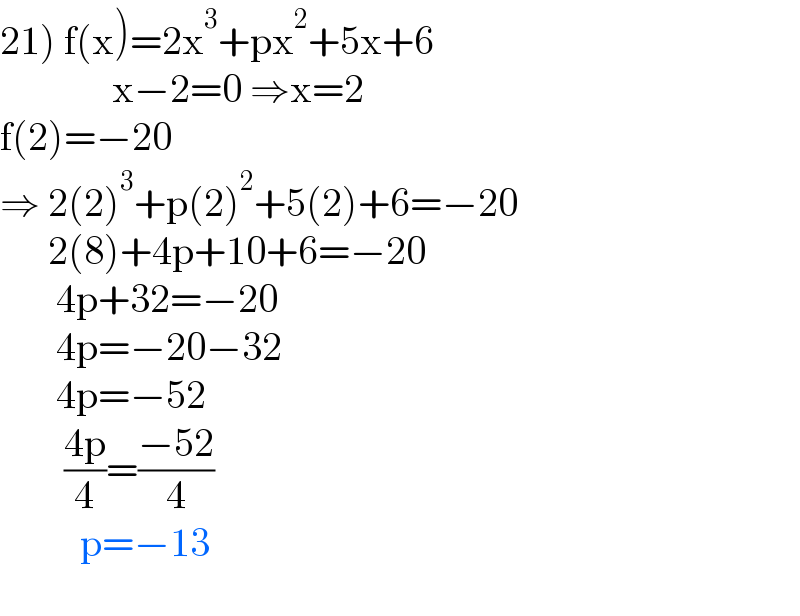
$$\left.\mathrm{21}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{3}} +\mathrm{px}^{\mathrm{2}} +\mathrm{5x}+\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}−\mathrm{2}=\mathrm{0}\:\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{2}\right)=−\mathrm{20} \\ $$$$\Rightarrow\:\mathrm{2}\left(\mathrm{2}\right)^{\mathrm{3}} +\mathrm{p}\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{5}\left(\mathrm{2}\right)+\mathrm{6}=−\mathrm{20} \\ $$$$\:\:\:\:\:\:\mathrm{2}\left(\mathrm{8}\right)+\mathrm{4p}+\mathrm{10}+\mathrm{6}=−\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\mathrm{4p}+\mathrm{32}=−\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\mathrm{4p}=−\mathrm{20}−\mathrm{32} \\ $$$$\:\:\:\:\:\:\:\mathrm{4p}=−\mathrm{52} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{4p}}{\mathrm{4}}=\frac{−\mathrm{52}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{p}=−\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\: \\ $$
