Question-157925

Question Number 157925 by cortano last updated on 29/Oct/21

Answered by FongXD last updated on 30/Oct/21

Given: ((sinαcosα)/(sinβcosβ))=(8/5) (1) and ((sinαcosβ)/(sinβcosα))=4 (2) ⇔ (1)∙(2): ((sin^2 α)/(sin^2 β))=((32)/5) and (1)÷(2): ((cos^2 α)/(cos^2 β))=(2/5) ⇔ 5−5sin^2 α=2−2sin^2 β but 5sin^2 α=32sin^2 β ⇔ 5−32sin^2 β=2−2sin^2 β ⇔ 30sin^2 β=3 ⇔ sinβ^2 =(1/(10)), ⇒ cos^2 β=(√((99)/(100)))=((3(√(11)))/(10)) we get: tanα+tanβ=5tanβ=±5(√((sin^2 β)/(cos^2 β)))=±(5/( (√(3(√(11))))))

$$\mathrm{Given}:\:\frac{\mathrm{sin}\alpha\mathrm{cos}\alpha}{\mathrm{sin}\beta\mathrm{cos}\beta}=\frac{\mathrm{8}}{\mathrm{5}}\:\:\:\left(\mathrm{1}\right)\:\mathrm{and}\:\frac{\mathrm{sin}\alpha\mathrm{cos}\beta}{\mathrm{sin}\beta\mathrm{cos}\alpha}=\mathrm{4}\:\:\:\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow\:\left(\mathrm{1}\right)\centerdot\left(\mathrm{2}\right):\:\frac{\mathrm{sin}^{\mathrm{2}} \alpha}{\mathrm{sin}^{\mathrm{2}} \beta}=\frac{\mathrm{32}}{\mathrm{5}}\:\mathrm{and}\:\left(\mathrm{1}\right)\boldsymbol{\div}\left(\mathrm{2}\right):\:\frac{\mathrm{cos}^{\mathrm{2}} \alpha}{\mathrm{cos}^{\mathrm{2}} \beta}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\Leftrightarrow\:\mathrm{5}−\mathrm{5sin}^{\mathrm{2}} \alpha=\mathrm{2}−\mathrm{2sin}^{\mathrm{2}} \beta \\ $$$$\mathrm{but}\:\mathrm{5sin}^{\mathrm{2}} \alpha=\mathrm{32sin}^{\mathrm{2}} \beta \\ $$$$\Leftrightarrow\:\mathrm{5}−\mathrm{32sin}^{\mathrm{2}} \beta=\mathrm{2}−\mathrm{2sin}^{\mathrm{2}} \beta \\ $$$$\Leftrightarrow\:\mathrm{30sin}^{\mathrm{2}} \beta=\mathrm{3} \\ $$$$\Leftrightarrow\:\mathrm{sin}\beta^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{10}},\:\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \beta=\sqrt{\frac{\mathrm{99}}{\mathrm{100}}}=\frac{\mathrm{3}\sqrt{\mathrm{11}}}{\mathrm{10}} \\ $$$$\mathrm{we}\:\mathrm{get}:\:\mathrm{tan}\alpha+\mathrm{tan}\beta=\mathrm{5tan}\beta=\pm\mathrm{5}\sqrt{\frac{\mathrm{sin}^{\mathrm{2}} \beta}{\mathrm{cos}^{\mathrm{2}} \beta}}=\pm\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}\sqrt{\mathrm{11}}}} \\ $$

Commented by cortano last updated on 30/Oct/21

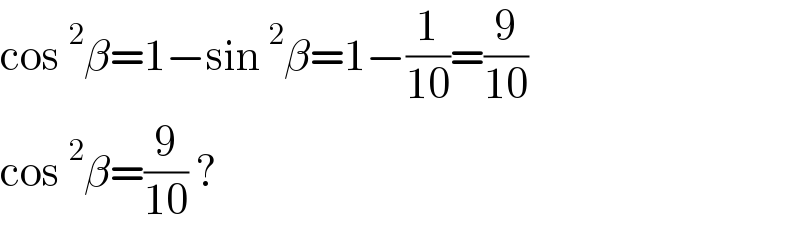
cos^2 β=1−sin^2 β=1−(1/(10))=(9/(10)) cos^2 β=(9/(10)) ?

$$\mathrm{cos}\:^{\mathrm{2}} \beta=\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \beta=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}=\frac{\mathrm{9}}{\mathrm{10}} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \beta=\frac{\mathrm{9}}{\mathrm{10}}\:? \\ $$

Commented by FongXD last updated on 30/Oct/21

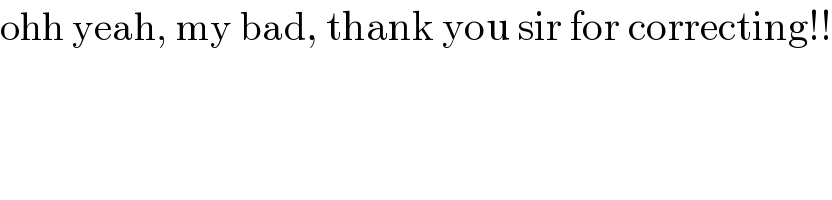
ohh yeah, my bad, thank you sir for correcting!!

$$\mathrm{ohh}\:\mathrm{yeah},\:\mathrm{my}\:\mathrm{bad},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{correcting}!! \\ $$

Commented by cortano last updated on 30/Oct/21

$${great}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply