Question Number 157942 by mathlove last updated on 30/Oct/21
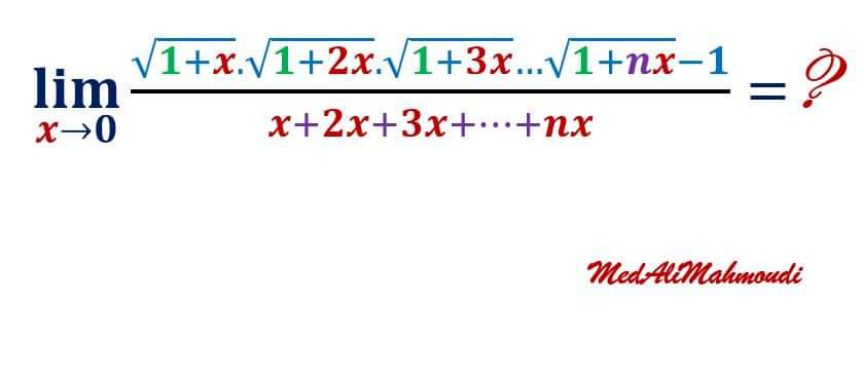
Commented by cortano last updated on 30/Oct/21
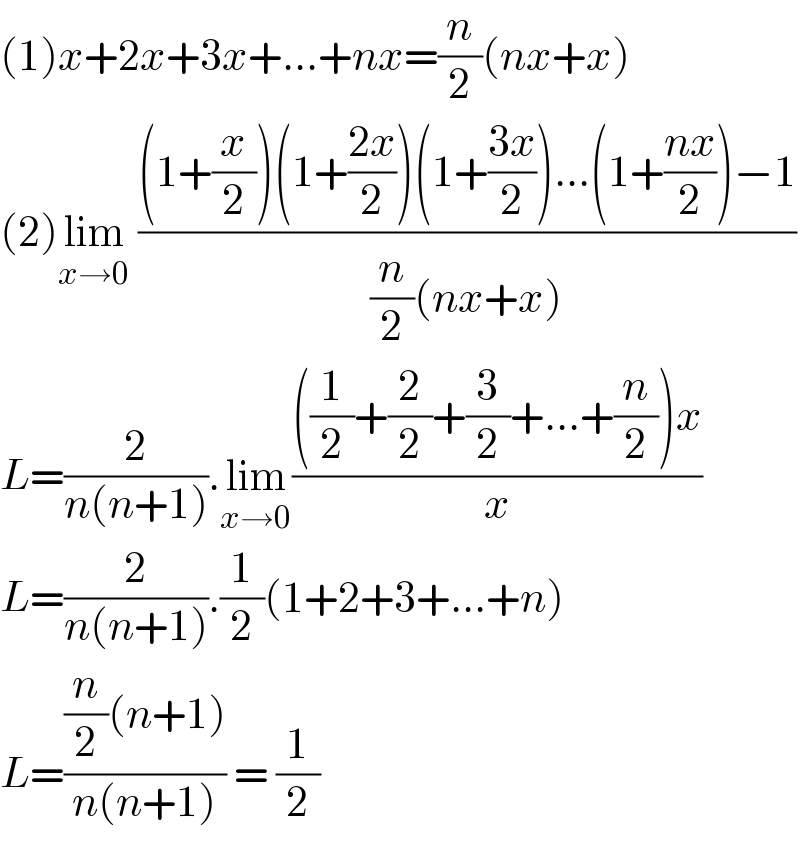
$$\left(\mathrm{1}\right){x}+\mathrm{2}{x}+\mathrm{3}{x}+…+{nx}=\frac{{n}}{\mathrm{2}}\left({nx}+{x}\right) \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2}}\right)…\left(\mathrm{1}+\frac{{nx}}{\mathrm{2}}\right)−\mathrm{1}}{\frac{{n}}{\mathrm{2}}\left({nx}+{x}\right)} \\ $$$${L}=\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}+…+\frac{{n}}{\mathrm{2}}\right){x}}{{x}} \\ $$$${L}=\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)}.\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}\right) \\ $$$${L}=\frac{\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right)}{{n}\left({n}+\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
