Question Number 157957 by HongKing last updated on 30/Oct/21
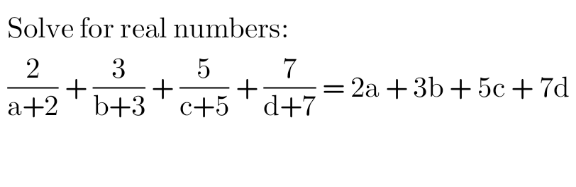
Commented by MJS_new last updated on 31/Oct/21
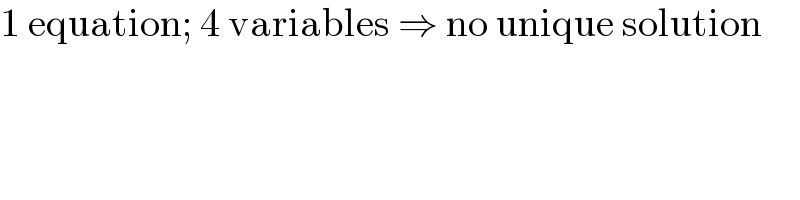
$$\mathrm{1}\:\mathrm{equation};\:\mathrm{4}\:\mathrm{variables}\:\Rightarrow\:\mathrm{no}\:\mathrm{unique}\:\mathrm{solution} \\ $$
Commented by HongKing last updated on 31/Oct/21

$$\mathrm{how}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}… \\ $$
Commented by MJS_new last updated on 31/Oct/21
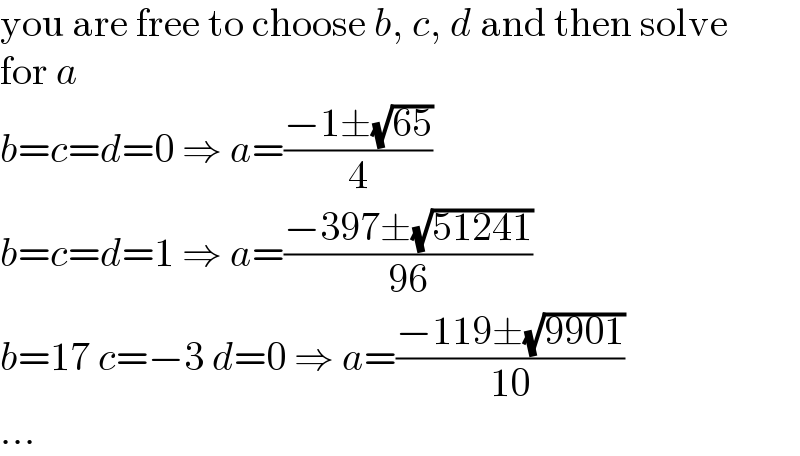
$$\mathrm{you}\:\mathrm{are}\:\mathrm{free}\:\mathrm{to}\:\mathrm{choose}\:{b},\:{c},\:{d}\:\mathrm{and}\:\mathrm{then}\:\mathrm{solve} \\ $$$$\mathrm{for}\:{a} \\ $$$${b}={c}={d}=\mathrm{0}\:\Rightarrow\:{a}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{65}}}{\mathrm{4}} \\ $$$${b}={c}={d}=\mathrm{1}\:\Rightarrow\:{a}=\frac{−\mathrm{397}\pm\sqrt{\mathrm{51241}}}{\mathrm{96}} \\ $$$${b}=\mathrm{17}\:{c}=−\mathrm{3}\:{d}=\mathrm{0}\:\Rightarrow\:{a}=\frac{−\mathrm{119}\pm\sqrt{\mathrm{9901}}}{\mathrm{10}} \\ $$$$… \\ $$
Answered by mr W last updated on 30/Oct/21
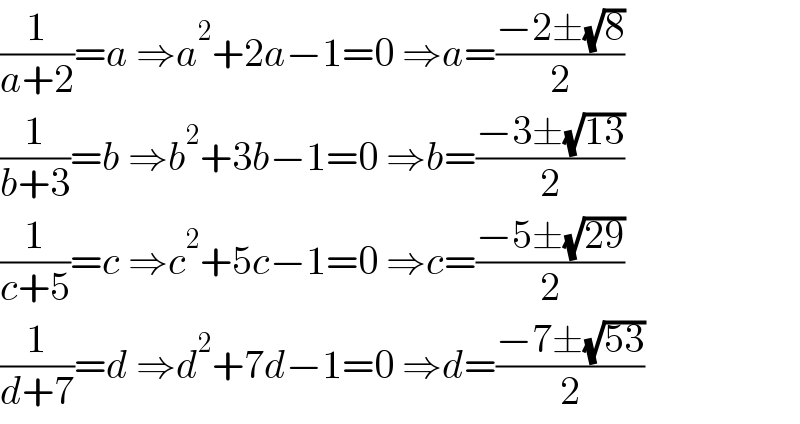
$$\frac{\mathrm{1}}{{a}+\mathrm{2}}={a}\:\Rightarrow{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{1}=\mathrm{0}\:\Rightarrow{a}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{8}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{b}+\mathrm{3}}={b}\:\Rightarrow{b}^{\mathrm{2}} +\mathrm{3}{b}−\mathrm{1}=\mathrm{0}\:\Rightarrow{b}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{c}+\mathrm{5}}={c}\:\Rightarrow{c}^{\mathrm{2}} +\mathrm{5}{c}−\mathrm{1}=\mathrm{0}\:\Rightarrow{c}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{29}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{d}+\mathrm{7}}={d}\:\Rightarrow{d}^{\mathrm{2}} +\mathrm{7}{d}−\mathrm{1}=\mathrm{0}\:\Rightarrow{d}=\frac{−\mathrm{7}\pm\sqrt{\mathrm{53}}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 30/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$$$\mathrm{But}\:\mathrm{please}\:\mathrm{check}\:\mathrm{again} \\ $$
Commented by mr W last updated on 30/Oct/21

$${there}\:{might}\:{be}\:{other}\:{solutions}. \\ $$$${if}\:{you}\:{know}\:{the}\:{solution},\:{please} \\ $$$${share}. \\ $$
