Question Number 158017 by cortano last updated on 30/Oct/21

Commented by tounghoungko last updated on 31/Oct/21
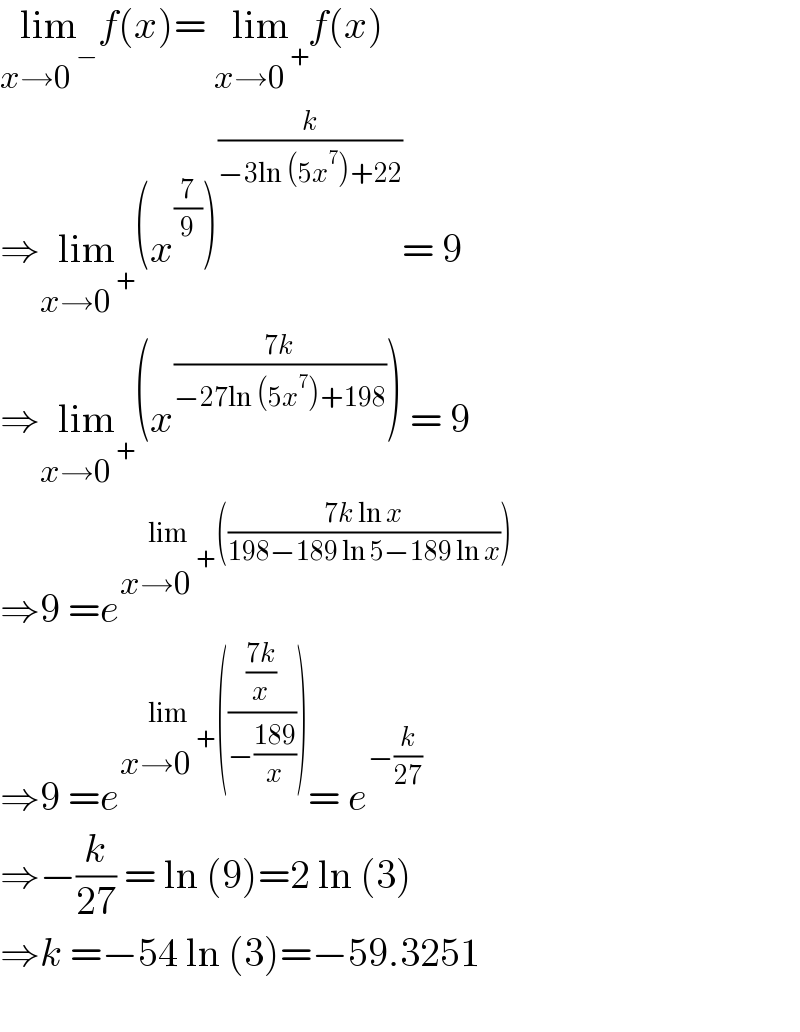
$$\underset{{x}\rightarrow\mathrm{0}^{\:−} } {\mathrm{lim}}{f}\left({x}\right)=\:\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}{f}\left({x}\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}\left({x}^{\frac{\mathrm{7}}{\mathrm{9}}} \right)^{\frac{{k}}{−\mathrm{3ln}\:\left(\mathrm{5}{x}^{\mathrm{7}} \right)+\mathrm{22}}} =\:\mathrm{9} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}\left({x}^{\frac{\mathrm{7}{k}}{−\mathrm{27ln}\:\left(\mathrm{5}{x}^{\mathrm{7}} \right)+\mathrm{198}}} \right)\:=\:\mathrm{9} \\ $$$$\Rightarrow\mathrm{9}\:={e}^{\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}\left(\frac{\mathrm{7}{k}\:\mathrm{ln}\:{x}}{\mathrm{198}−\mathrm{189}\:\mathrm{ln}\:\mathrm{5}−\mathrm{189}\:\mathrm{ln}\:{x}}\right)} \\ $$$$\Rightarrow\mathrm{9}\:={e}^{\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}\left(\frac{\frac{\mathrm{7}{k}}{{x}}}{−\frac{\mathrm{189}}{{x}}}\right)} =\:{e}^{−\frac{{k}}{\mathrm{27}}} \\ $$$$\Rightarrow−\frac{{k}}{\mathrm{27}}\:=\:\mathrm{ln}\:\left(\mathrm{9}\right)=\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{3}\right) \\ $$$$\Rightarrow{k}\:=−\mathrm{54}\:\mathrm{ln}\:\left(\mathrm{3}\right)=−\mathrm{59}.\mathrm{3251} \\ $$$$ \\ $$
