Question Number 158069 by zainaltanjung last updated on 30/Oct/21
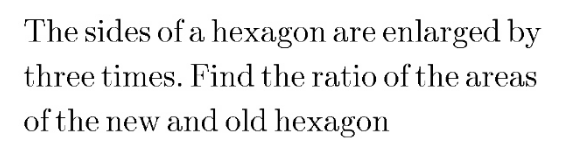
Answered by Rasheed.Sindhi last updated on 30/Oct/21

$${Let}\:{the}\:{side}\:{of}\:\:{old}\:\:{hexagon}={a} \\ $$$$\blacktriangle_{{old}} =\mathrm{6}\sqrt{\frac{\mathrm{3}{a}}{\mathrm{2}}\left(\frac{\mathrm{3}{a}}{\mathrm{2}}−{a}\right)^{\mathrm{3}} } \\ $$$$\blacktriangle_{{old}} =\mathrm{6}\sqrt{\frac{\mathrm{3}{a}}{\mathrm{2}}\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{3}} }\:=\mathrm{6}\sqrt{\mathrm{3}\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{6}\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \sqrt{\mathrm{3}}=\mathrm{6}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)\sqrt{\mathrm{3}}=\frac{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${Side}\:{of}\:{new}\:\mathrm{6}-{gon}=\mathrm{3}{a} \\ $$$$\blacktriangle_{{new}} =\mathrm{6}\sqrt{\frac{\mathrm{9}{a}}{\mathrm{2}}\left(\frac{\mathrm{9}{a}}{\mathrm{2}}−\mathrm{3}{a}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{6}\sqrt{\frac{\mathrm{9}{a}}{\mathrm{2}}\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{\mathrm{3}} }\:=\mathrm{6}\sqrt{\mathrm{3}\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{6}\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{\mathrm{2}} \sqrt{\mathrm{3}}\:=\mathrm{6}\left(\frac{\mathrm{9}{a}^{\mathrm{2}} }{\mathrm{4}}\right)\sqrt{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{27}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\frac{\blacktriangle_{{new}} }{\blacktriangle_{{old}} }=\frac{\frac{\mathrm{27}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\mathrm{27}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}=\frac{\mathrm{9}}{\mathrm{1}}=\mathrm{9}:\mathrm{1} \\ $$
