Menu Close

Question-158079

Tinku Tara 0 Comments
Pin




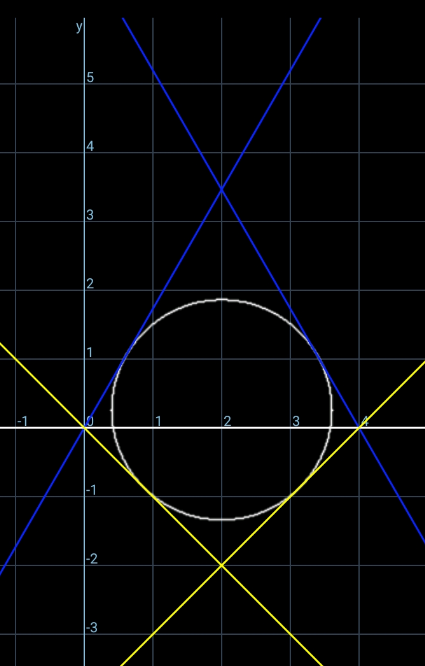
Question Number 158079 by ajfour last updated on 30/Oct/21
Commented by ajfour last updated on 31/Oct/21
Sir, the question should state: find sum of radii (in terms of sides of △ABC) that touch two sides of the said △ABC and outer sides of right angled △ constructed with the third side of △ABC as the hypotenuse. q(a,b,c)=r_A +r_B +r_C .
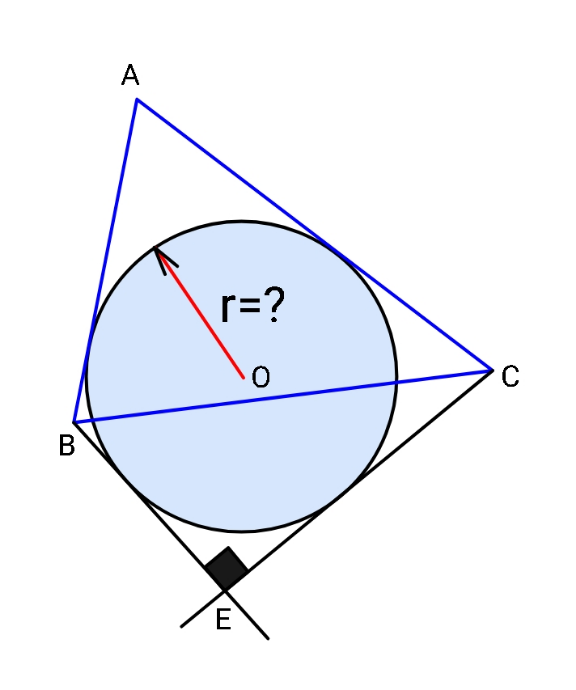
$${Sir},\:{the}\:{question}\:{should}\:{state}: \\ $$$${find}\:{sum}\:{of}\:{radii}\:\left({in}\:{terms}\:{of}\right. \\ $$$$\left.{sides}\:{of}\:\bigtriangleup{ABC}\right)\:{that}\:{touch} \\ $$$${two}\:{sides}\:{of}\:{the}\:{said}\:\bigtriangleup{ABC} \\ $$$${and}\:{outer}\:{sides}\:{of}\:{right}\:{angled} \\ $$$$\bigtriangleup\:{constructed}\:{with}\:{the}\:{third} \\ $$$${side}\:{of}\:\bigtriangleup{ABC}\:{as}\:{the}\:{hypotenuse}. \\ $$$${q}\left({a},{b},{c}\right)={r}_{{A}} +{r}_{{B}} +{r}_{{C}} \:\:. \\ $$
Answered by mr W last updated on 31/Oct/21
Commented by mr W last updated on 01/Nov/21
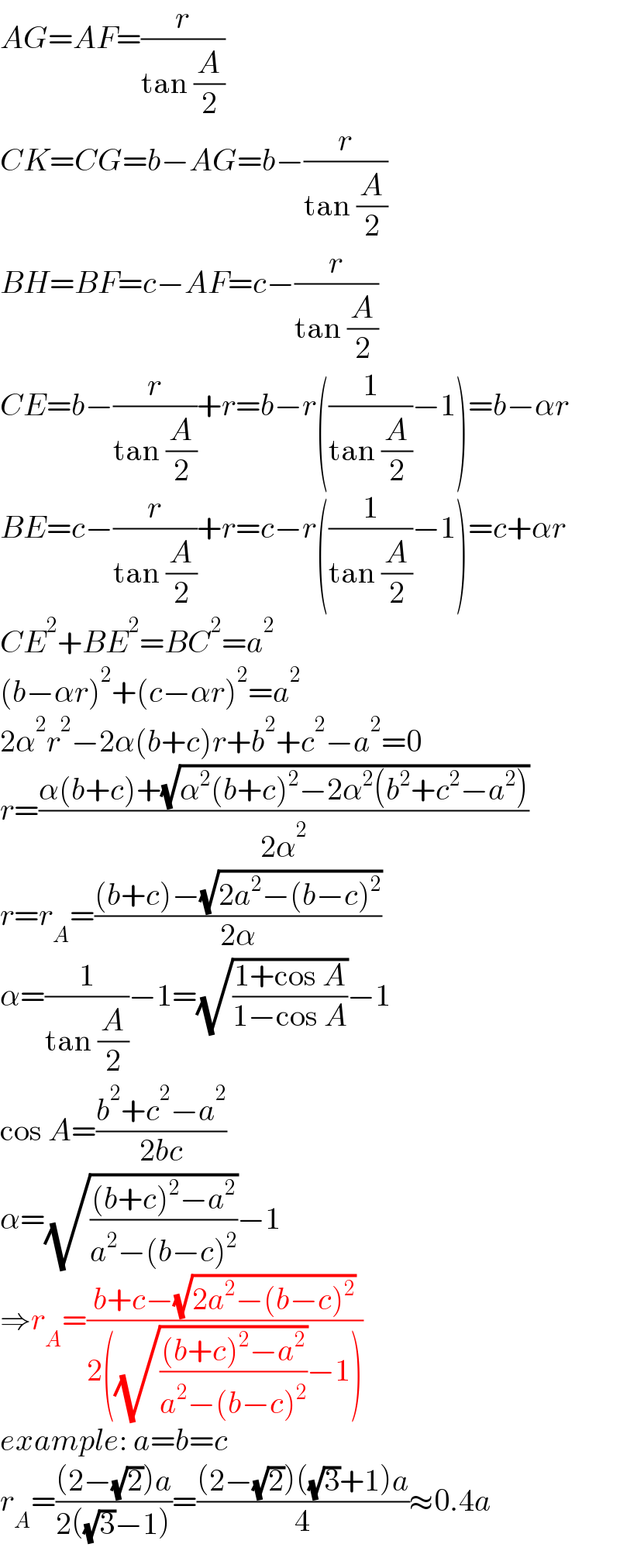
AG=AF=(r/(tan (A/2))) CK=CG=b−AG=b−(r/(tan (A/2))) BH=BF=c−AF=c−(r/(tan (A/2))) CE=b−(r/(tan (A/2)))+r=b−r((1/(tan (A/2)))−1)=b−αr BE=c−(r/(tan (A/2)))+r=c−r((1/(tan (A/2)))−1)=c+αr CE^2 +BE^2 =BC^2 =a^2 (b−αr)^2 +(c−αr)^2 =a^2 2α^2 r^2 −2α(b+c)r+b^2 +c^2 −a^2 =0 r=((α(b+c)+(√(α^2 (b+c)^2 −2α^2 (b^2 +c^2 −a^2 ))))/(2α^2 )) r=r_A =(((b+c)−(√(2a^2 −(b−c)^2 )))/(2α)) α=(1/(tan (A/2)))−1=(√((1+cos A)/(1−cos A)))−1 cos A=((b^2 +c^2 −a^2 )/(2bc)) α=(√(((b+c)^2 −a^2 )/(a^2 −(b−c)^2 )))−1 ⇒r_A =((b+c−(√(2a^2 −(b−c)^2 )))/(2((√(((b+c)^2 −a^2 )/(a^2 −(b−c)^2 )))−1))) example: a=b=c r_A =(((2−(√2))a)/(2((√3)−1)))=(((2−(√2))((√3)+1)a)/4)≈0.4a
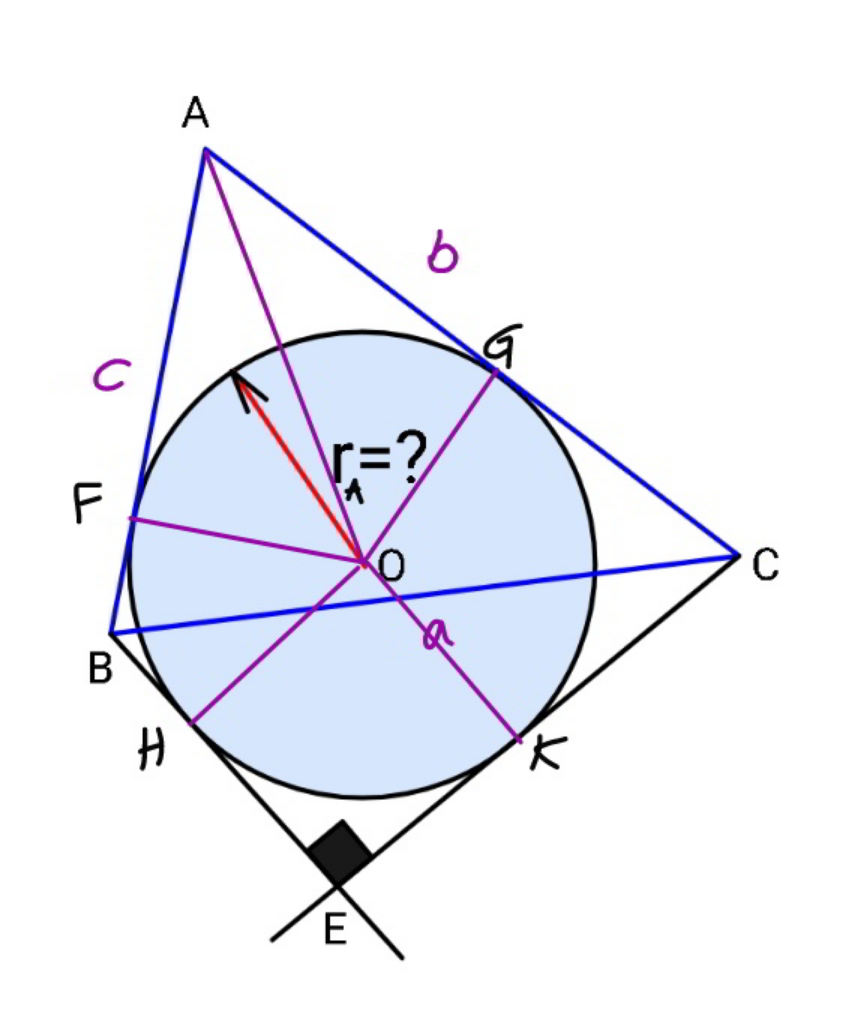
$${AG}={AF}=\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}} \\ $$$${CK}={CG}={b}−{AG}={b}−\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}} \\ $$$${BH}={BF}={c}−{AF}={c}−\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}} \\ $$$${CE}={b}−\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}+{r}={b}−{r}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}−\mathrm{1}\right)={b}−\alpha{r} \\ $$$${BE}={c}−\frac{{r}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}+{r}={c}−{r}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}−\mathrm{1}\right)={c}+\alpha{r} \\ $$$${CE}^{\mathrm{2}} +{BE}^{\mathrm{2}} ={BC}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left({b}−\alpha{r}\right)^{\mathrm{2}} +\left({c}−\alpha{r}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{2}\alpha^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{2}\alpha\left({b}+{c}\right){r}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${r}=\frac{\alpha\left({b}+{c}\right)+\sqrt{\alpha^{\mathrm{2}} \left({b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\alpha^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{\mathrm{2}\alpha^{\mathrm{2}} } \\ $$$${r}={r}_{{A}} =\frac{\left({b}+{c}\right)−\sqrt{\mathrm{2}{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }}{\mathrm{2}\alpha} \\ $$$$\alpha=\frac{\mathrm{1}}{\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}−\mathrm{1}=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:{A}}{\mathrm{1}−\mathrm{cos}\:{A}}}−\mathrm{1} \\ $$$$\mathrm{cos}\:{A}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$$\alpha=\sqrt{\frac{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }}−\mathrm{1} \\ $$$$\Rightarrow{r}_{{A}} =\frac{{b}+{c}−\sqrt{\mathrm{2}{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }}{\mathrm{2}\left(\sqrt{\frac{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }}−\mathrm{1}\right)} \\ $$$${example}:\:{a}={b}={c} \\ $$$${r}_{{A}} =\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){a}}{\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{3}}+\mathrm{1}\right){a}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{4}{a} \\ $$
Commented by ajfour last updated on 01/Nov/21
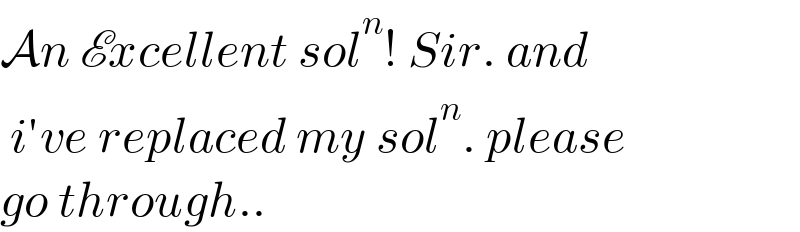
An Excellent sol^n ! Sir. and i′ve replaced my sol^n . please go through..
$$\mathcal{A}{n}\:\mathscr{E}{xcellent}\:{sol}^{{n}} !\:{Sir}.\:{and} \\ $$$$\:{i}'{ve}\:{replaced}\:{my}\:{sol}^{{n}} .\:{please} \\ $$$${go}\:{through}.. \\ $$
Commented by mr W last updated on 01/Nov/21
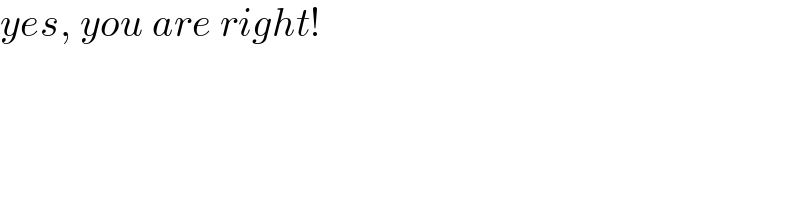
yes, you are right!
$${yes},\:{you}\:{are}\:{right}! \\ $$
Commented by ajfour last updated on 01/Nov/21
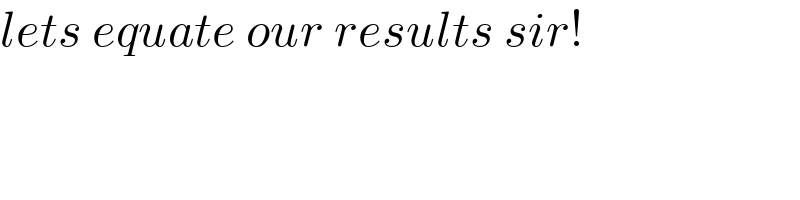
lets equate our results sir!
$${lets}\:{equate}\:{our}\:{results}\:{sir}! \\ $$
Answered by ajfour last updated on 31/Oct/21
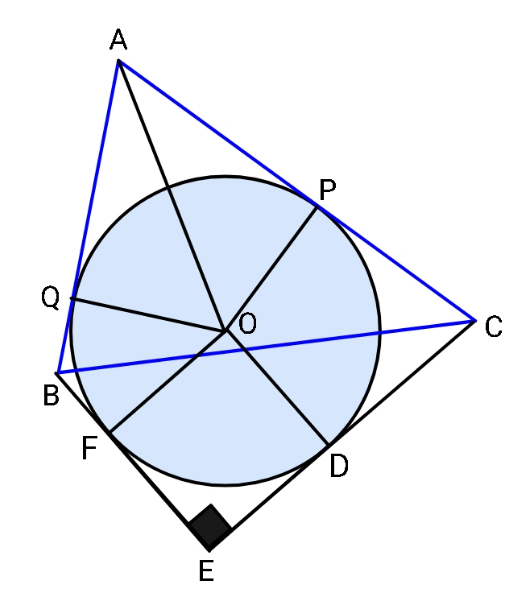
Commented by ajfour last updated on 01/Nov/21
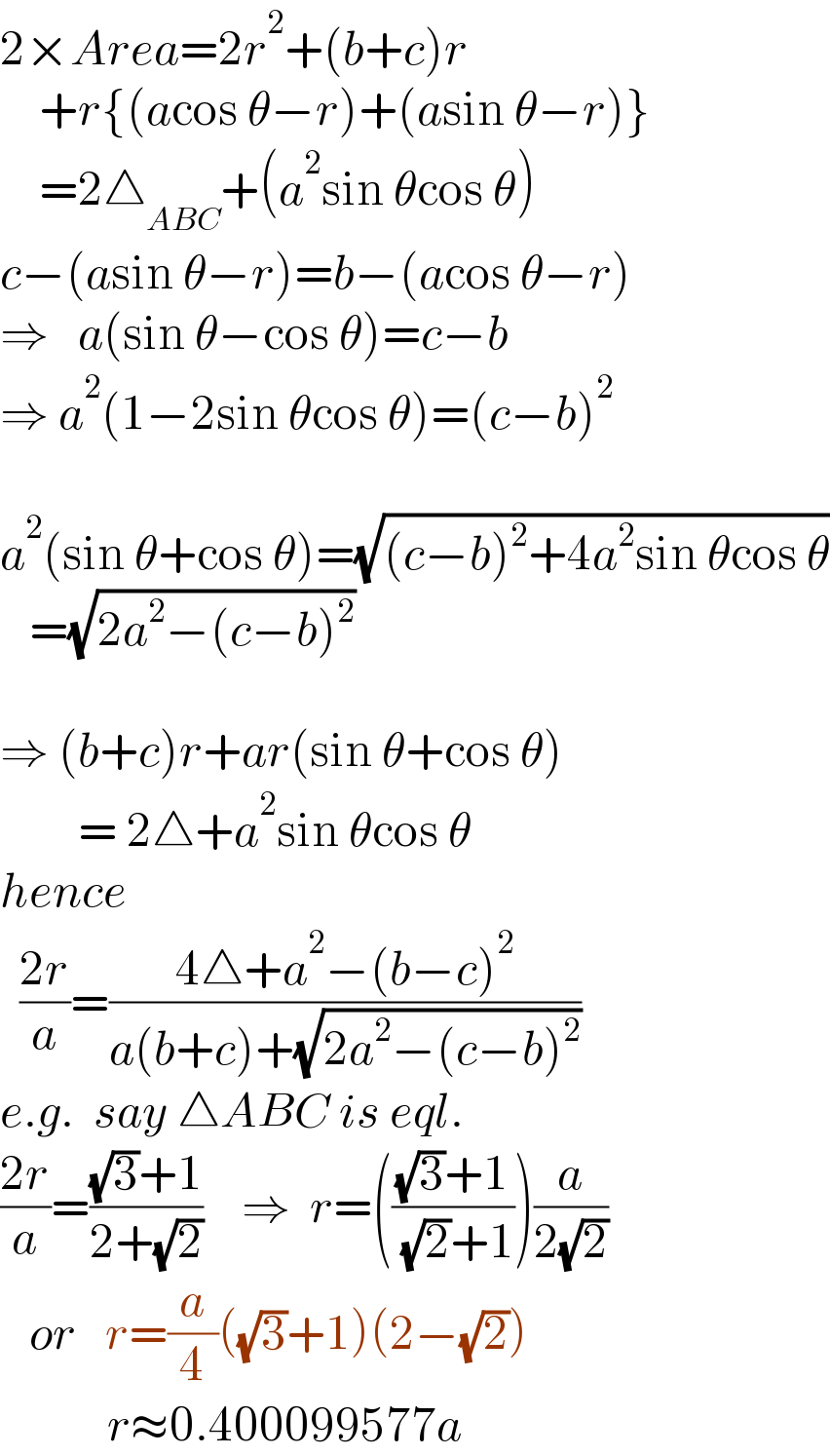
2×Area=2r^2 +(b+c)r +r{(acos θ−r)+(asin θ−r)} =2△_(ABC) +(a^2 sin θcos θ) c−(asin θ−r)=b−(acos θ−r) ⇒ a(sin θ−cos θ)=c−b ⇒ a^2 (1−2sin θcos θ)=(c−b)^2 a^2 (sin θ+cos θ)=(√((c−b)^2 +4a^2 sin θcos θ)) =(√(2a^2 −(c−b)^2 )) ⇒ (b+c)r+ar(sin θ+cos θ) = 2△+a^2 sin θcos θ hence ((2r)/a)=((4△+a^2 −(b−c)^2 )/(a(b+c)+(√(2a^2 −(c−b)^2 )))) e.g. say △ABC is eql. ((2r)/a)=(((√3)+1)/(2+(√2))) ⇒ r=((((√3)+1)/( (√2)+1)))(a/(2(√2))) or r=(a/4)((√3)+1)(2−(√2)) r≈0.400099577a
$$\mathrm{2}×{Area}=\mathrm{2}{r}^{\mathrm{2}} +\left({b}+{c}\right){r} \\ $$$$\:\:\:\:+{r}\left\{\left({a}\mathrm{cos}\:\theta−{r}\right)+\left({a}\mathrm{sin}\:\theta−{r}\right)\right\} \\ $$$$\:\:\:\:=\mathrm{2}\bigtriangleup_{{ABC}} +\left({a}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta\right) \\ $$$${c}−\left({a}\mathrm{sin}\:\theta−{r}\right)={b}−\left({a}\mathrm{cos}\:\theta−{r}\right) \\ $$$$\Rightarrow\:\:\:{a}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)={c}−{b} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\right)=\left({c}−{b}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${a}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)=\sqrt{\left({c}−{b}\right)^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta} \\ $$$$\:\:\:=\sqrt{\mathrm{2}{a}^{\mathrm{2}} −\left({c}−{b}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\Rightarrow\:\left({b}+{c}\right){r}+{ar}\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{2}\bigtriangleup+{a}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${hence} \\ $$$$\:\:\frac{\mathrm{2}{r}}{{a}}=\frac{\mathrm{4}\bigtriangleup+{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }{{a}\left({b}+{c}\right)+\sqrt{\mathrm{2}{a}^{\mathrm{2}} −\left({c}−{b}\right)^{\mathrm{2}} }} \\ $$$${e}.{g}.\:\:{say}\:\bigtriangleup{ABC}\:{is}\:{eql}. \\ $$$$\frac{\mathrm{2}{r}}{{a}}=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:\:\:\:\Rightarrow\:\:{r}=\left(\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right)\frac{{a}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\:\:{or}\:\:\:{r}=\frac{{a}}{\mathrm{4}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\left(\mathrm{2}−\sqrt{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{r}\approx\mathrm{0}.\mathrm{400099577}{a} \\ $$
Commented by ajfour last updated on 01/Nov/21

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *