Question Number 158182 by Eric002 last updated on 31/Oct/21
Commented by Eric002 last updated on 31/Oct/21
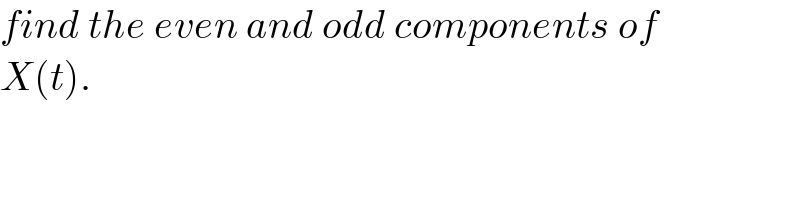
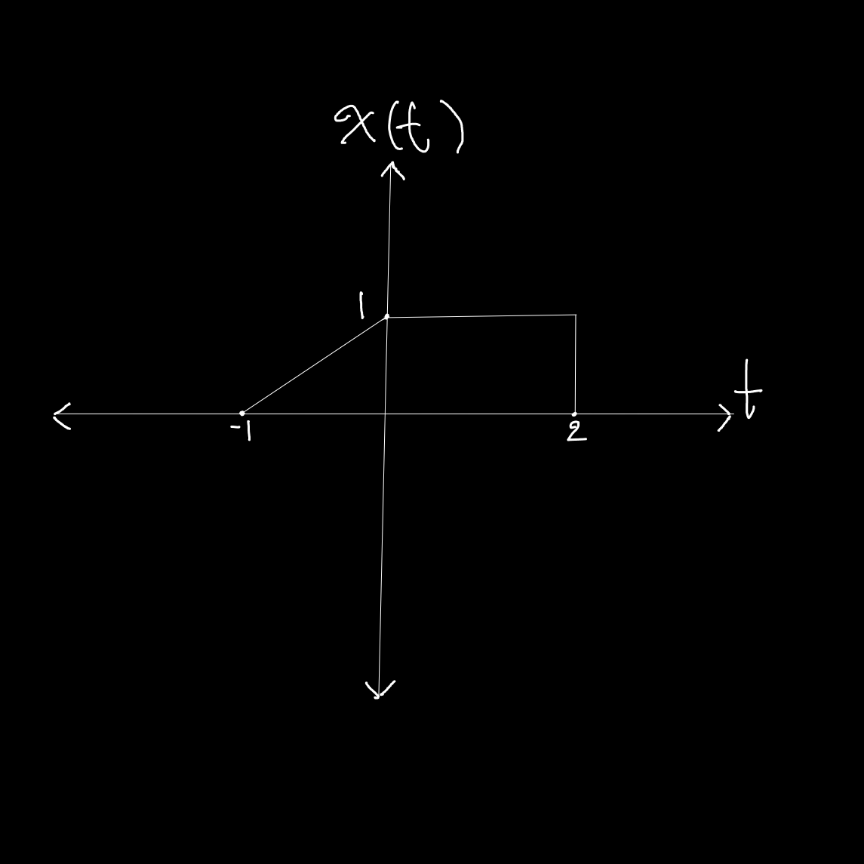
$${find}\:{the}\:{even}\:{and}\:{odd}\:{components}\:{of} \\ $$$${X}\left({t}\right). \\ $$
Answered by aleks041103 last updated on 05/Nov/21
![given a function f(x) we can decompose it in an even and odd functions e(x) and o(x): f(x)=e(x)+o(x) ⇒f(−x)=e(−x)+o(−x)=e(x)−o(x) ⇒e(x)=(1/2)(f(x)+f(−x)) o(x)=(1/2)(f(x)−f(−x)) Now: x(t)= { ((0, t∈(−∞,−1]∪[2,∞))),((1+t, t∈(−1,0])),((1, t∈(0,2))) :}= { ((0, t∈(−∞,−2]∪[2,∞))),((0, t∈(−2,−1])),((1+t, t∈(−1,0))),((1, t∈[0,1))),((1,t∈[1,2))) :} and x(−t)= { ((0, t∈(−∞,−2]∪[1,∞))),((1−t, t∈[0,1))),((1, t∈(−2,0))) :}= { ((0, t∈(−∞,−2]∪[2,∞))),((1, t∈(−2,−1])),((1, t∈(−1,0))),((1−t, t∈[0,1))),((0,t∈[1,2))) :} Then: e(t)=(1/2)(x(t)+x(−t)) e(t)=(1/2)( { ((0, t∈(−∞,−2]∪[2,∞))),((0, t∈(−2,−1])),((1+t, t∈(−1,0))),((1, t∈[0,1))),((1,t∈[1,2))) :}+ { ((0, t∈(−∞,−2]∪[2,∞))),((1, t∈(−2,−1])),((1, t∈(−1,0))),((1−t, t∈[0,1))),((0,t∈[1,2))) :})= =(1/2) { ((0+0, t∈(−∞,−2]∪[2,∞))),((0+1, t∈(−2,−1])),((1+t+1, t∈(−1,0))),((1+1−t, t∈[0,1))),((1+0,t∈[1,2))) :}= = { ((0, t∈(−∞,−2]∪[2,∞))),((1/2, t∈(−2,−1])),((1+t/2, t∈(−1,0))),((1−t/2, t∈[0,1))),((1/2,t∈[1,2))) :}= { ((1−(t/2),t∈[0,1))),((1/2, t∈[1,2))),((0, t∈[2,∞))),((e(−t),t<0)) :} ⇒e(t)= { ((1−(t/2),t∈[0,1))),((1/2, t∈[1,2))),((0, t∈[2,∞))),((e(−t),t<0)) :} o(t)=(1/2)(x(t)−x(−t))= =(1/2)( { ((0, t∈(−∞,−2]∪[2,∞))),((0, t∈(−2,−1])),((1+t, t∈(−1,0))),((1, t∈[0,1))),((1,t∈[1,2))) :}+ { ((0, t∈(−∞,−2]∪[2,∞))),((1, t∈(−2,−1])),((1, t∈(−1,0))),((1−t, t∈[0,1))),((0,t∈[1,2))) :}) =(1/2) { ((0−0, t∈(−∞,−2]∪[2,∞))),((0−1, t∈(−2,−1])),((1+t−1, t∈(−1,0))),((1−1+t, t∈[0,1))),((1−0,t∈[1,2))) :}= = { ((0, t∈(−∞,−2]∪[2,∞))),((−1/2, t∈(−2,−1])),((t/2, t∈(−1,0))),((t/2, t∈[0,1))),((1/2,t∈[1,2))) :}= { (((t/2),t∈[0,1))),((1/2, t∈[1,2))),((0, t∈[2,∞))),((−o(−t),t<0)) :} ⇒o(t)= { (((t/2),t∈[0,1))),((1/2, t∈[1,2))),((0, t∈[2,∞))),((−o(−t),t<0)) :}](https://www.tinkutara.com/question/Q158509.png)
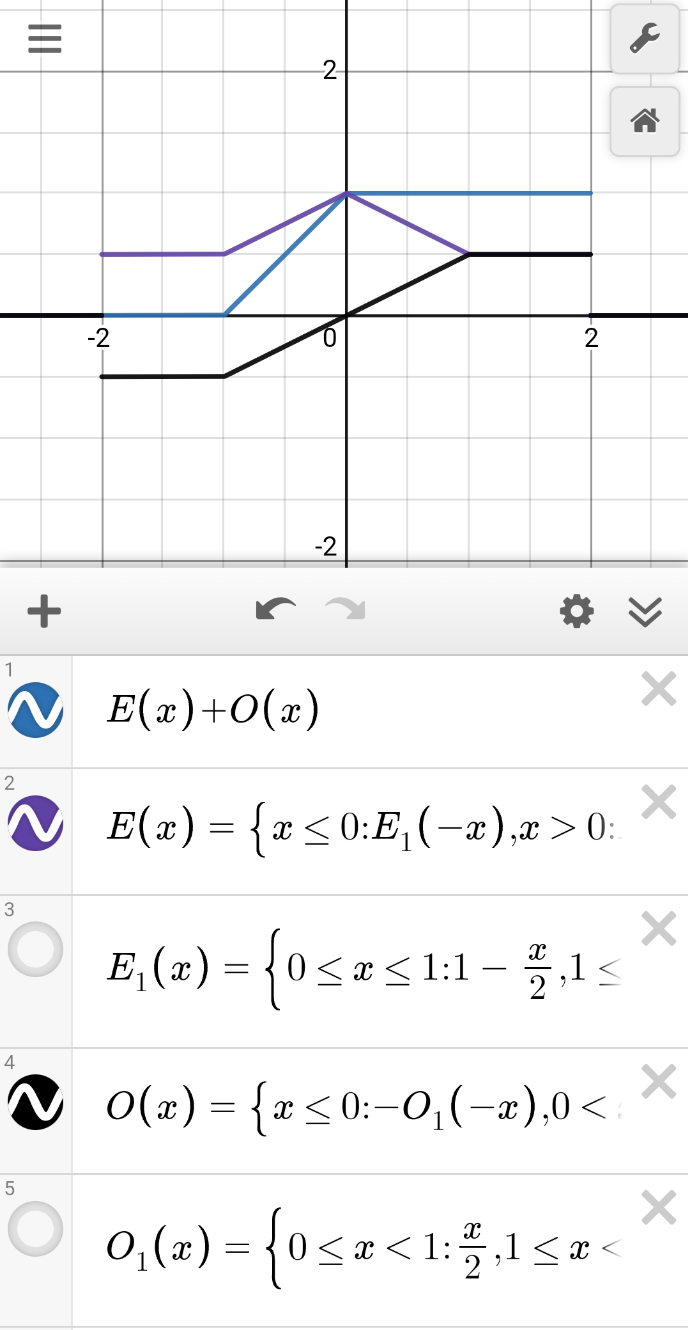
$${given}\:{a}\:{function}\:{f}\left({x}\right)\:{we}\:{can}\:{decompose} \\ $$$${it}\:{in}\:{an}\:{even}\:{and}\:{odd}\:{functions}\:{e}\left({x}\right)\:{and}\:{o}\left({x}\right): \\ $$$${f}\left({x}\right)={e}\left({x}\right)+{o}\left({x}\right) \\ $$$$\Rightarrow{f}\left(−{x}\right)={e}\left(−{x}\right)+{o}\left(−{x}\right)={e}\left({x}\right)−{o}\left({x}\right) \\ $$$$\Rightarrow{e}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({f}\left({x}\right)+{f}\left(−{x}\right)\right) \\ $$$${o}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({f}\left({x}\right)−{f}\left(−{x}\right)\right) \\ $$$${Now}: \\ $$$${x}\left({t}\right)=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{1}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{1}+{t},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right]}\\{\mathrm{1},\:{t}\in\left(\mathrm{0},\mathrm{2}\right)}\end{cases}=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{0},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases} \\ $$$${and} \\ $$$${x}\left(−{t}\right)=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{1},\infty\right)}\\{\mathrm{1}−{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1},\:{t}\in\left(−\mathrm{2},\mathrm{0}\right)}\end{cases}=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{1},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}−{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{0},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases} \\ $$$${Then}: \\ $$$${e}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\left({t}\right)+{x}\left(−{t}\right)\right) \\ $$$${e}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{0},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}+\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{1},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}−{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{0},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{cases}{\mathrm{0}+\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{0}+\mathrm{1},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t}+\mathrm{1},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}+\mathrm{1}−{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}+\mathrm{0},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}= \\ $$$$=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{1}/\mathrm{2},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t}/\mathrm{2},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}−{t}/\mathrm{2},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}=\begin{cases}{\mathrm{1}−\frac{{t}}{\mathrm{2}},{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},\:{t}\in\left[\mathrm{1},\mathrm{2}\right)}\\{\mathrm{0},\:{t}\in\left[\mathrm{2},\infty\right)}\\{{e}\left(−{t}\right),{t}<\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{e}\left({t}\right)=\begin{cases}{\mathrm{1}−\frac{{t}}{\mathrm{2}},{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},\:{t}\in\left[\mathrm{1},\mathrm{2}\right)}\\{\mathrm{0},\:{t}\in\left[\mathrm{2},\infty\right)}\\{{e}\left(−{t}\right),{t}<\mathrm{0}}\end{cases} \\ $$$${o}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\left({t}\right)−{x}\left(−{t}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{0},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}+\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{1},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}−{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{0},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{cases}{\mathrm{0}−\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{\mathrm{0}−\mathrm{1},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{\mathrm{1}+{t}−\mathrm{1},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{\mathrm{1}−\mathrm{1}+{t},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}−\mathrm{0},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}= \\ $$$$=\begin{cases}{\mathrm{0},\:{t}\in\left(−\infty,−\mathrm{2}\right]\cup\left[\mathrm{2},\infty\right)}\\{−\mathrm{1}/\mathrm{2},\:{t}\in\left(−\mathrm{2},−\mathrm{1}\right]}\\{{t}/\mathrm{2},\:{t}\in\left(−\mathrm{1},\mathrm{0}\right)}\\{{t}/\mathrm{2},\:{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},{t}\in\left[\mathrm{1},\mathrm{2}\right)}\end{cases}=\begin{cases}{\frac{{t}}{\mathrm{2}},{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},\:{t}\in\left[\mathrm{1},\mathrm{2}\right)}\\{\mathrm{0},\:{t}\in\left[\mathrm{2},\infty\right)}\\{−{o}\left(−{t}\right),{t}<\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{o}\left({t}\right)=\begin{cases}{\frac{{t}}{\mathrm{2}},{t}\in\left[\mathrm{0},\mathrm{1}\right)}\\{\mathrm{1}/\mathrm{2},\:{t}\in\left[\mathrm{1},\mathrm{2}\right)}\\{\mathrm{0},\:{t}\in\left[\mathrm{2},\infty\right)}\\{−{o}\left(−{t}\right),{t}<\mathrm{0}}\end{cases} \\ $$
Commented by Eric002 last updated on 05/Nov/21

$${well}\:{done}\:{sir}\: \\ $$
Commented by aleks041103 last updated on 05/Nov/21