Question-158185

Question Number 158185 by HongKing last updated on 31/Oct/21

Commented by MJS_new last updated on 31/Oct/21

$$\mathrm{obviously}\:{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$

Commented by HongKing last updated on 31/Oct/21

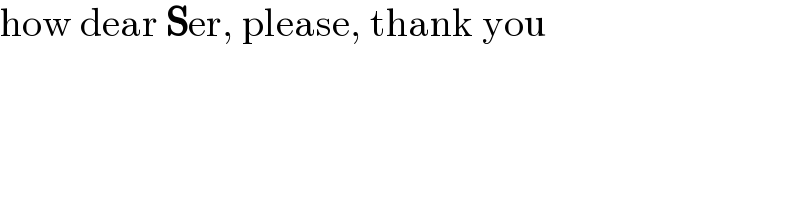
$$\mathrm{how}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{please},\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by MJS_new last updated on 31/Oct/21

with x=1 we have x^3 =1 ((x−1)/(x^3 +1))=(0/2)=0 ((x^3 (x+1))/(x^4 +1))=(2/2)=1 (((x−1)(x^2 +1))/x^4 )=(0/1)=0 ⇒ 1+0=1+0 true

$$\mathrm{with}\:{x}=\mathrm{1}\:\mathrm{we}\:\mathrm{have} \\ $$$${x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\frac{{x}−\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{2}}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)}{{x}^{\mathrm{4}} +\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$$$\frac{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} }=\frac{\mathrm{0}}{\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}+\mathrm{0}=\mathrm{1}+\mathrm{0}\:{true} \\ $$

Commented by HongKing last updated on 01/Nov/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{cool} \\ $$

Commented by MJS_new last updated on 01/Nov/21

there might be other solutions but this turns into a polynome of 12^(th) degree...

$$\mathrm{there}\:\mathrm{might}\:\mathrm{be}\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{but}\:\mathrm{this}\:\mathrm{turns} \\ $$$$\mathrm{into}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{12}^{\mathrm{th}} \:\mathrm{degree}… \\ $$

Commented by HongKing last updated on 01/Nov/21

$$\mathrm{yes}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$

Commented by MJS_new last updated on 01/Nov/21

I found 2 more real solutions x≈−1.41949255805 x≈−.864853259707 and 10 complex solutions exist

$$\mathrm{I}\:\mathrm{found}\:\mathrm{2}\:\mathrm{more}\:\mathrm{real}\:\mathrm{solutions} \\ $$$${x}\approx−\mathrm{1}.\mathrm{41949255805} \\ $$$${x}\approx−.\mathrm{864853259707} \\ $$$$\mathrm{and}\:\mathrm{10}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{exist} \\ $$

Commented by HongKing last updated on 01/Nov/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply