Question Number 158255 by daus last updated on 01/Nov/21
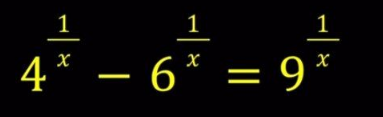
Commented by daus last updated on 01/Nov/21

$${solve}\:{the}\:{x} \\ $$$$ \\ $$
Commented by cortano last updated on 01/Nov/21
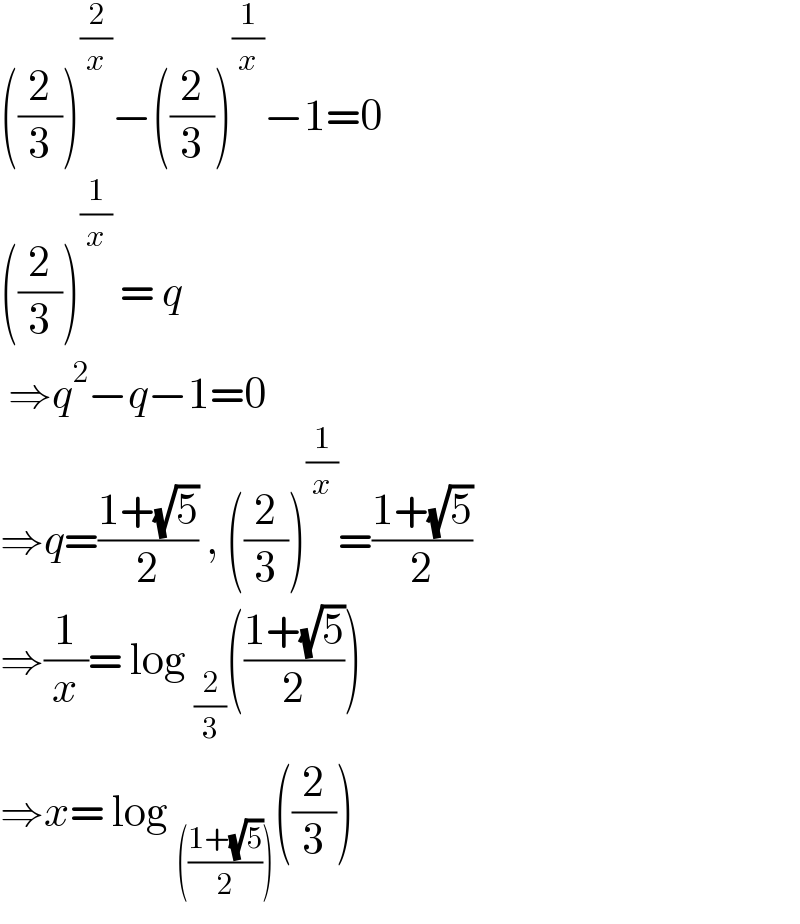
$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{2}}{{x}}} −\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{{x}}} \:=\:{q} \\ $$$$\:\Rightarrow{q}^{\mathrm{2}} −{q}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{q}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:,\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{{x}}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}=\:\mathrm{log}\:_{\frac{\mathrm{2}}{\mathrm{3}}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=\:\mathrm{log}\:_{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$
Answered by MathsFan last updated on 01/Nov/21
![(4^(1/x) /4^(1/x) )−(6^(1/x) /4^(1/x) )=(9^(1/x) /4^(1/x) ) 1−((3^(1/x) •2^(1/x) )/(2^(1/x) •2^(1/x) ))=(3^((1/x)•2) /2^((1/x)•2) ) 1−((3^(1/x) /2^(1/x) ))=((3^(1/x) /2^(1/x) ))^2 ((3^(1/x) /2^(1/x) ))^2 +((3^(1/x) /2^(1/x) ))=1 ((3^(1/x) /2^(1/x) ))^2 +((3^(1/x) /2^(1/x) ))+(1/4)=1+(1/4) [((3^(1/x) /2^(1/x) ))+(1/2)]^2 =(5/4) ((3^(1/x) /2^(1/x) ))=((±(√5))/2)−(1/2) ln((3/2))^(1/x) =ln(((√5)−1)/2) (1/x)=((ln(((√5)−1)/2))/(ln((3/2)))) x_1 =((ln((3/2)))/(ln(((√5)−1)/2))) x_2 =((ln((3/2)))/(ln((−(√5)−1)/2)))](https://www.tinkutara.com/question/Q158266.png)
$$\frac{\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{x}}} }−\frac{\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{x}}} }=\frac{\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{x}}} } \\ $$$$\:\mathrm{1}−\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} \bullet\cancel{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} \bullet\cancel{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }}=\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}\bullet\mathrm{2}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}\bullet\mathrm{2}} } \\ $$$$\:\mathrm{1}−\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)=\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)^{\mathrm{2}} \\ $$$$\:\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)=\mathrm{1} \\ $$$$\: \\ $$$$\:\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\left[\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)+\frac{\mathrm{1}}{\mathrm{2}}\right]^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\:\left(\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} }\right)=\frac{\pm\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\mathrm{ln}\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{ln}\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}{\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\:\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{ln}\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\:\:\:\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{ln}\frac{−\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}} \\ $$
Answered by yeti123 last updated on 01/Nov/21
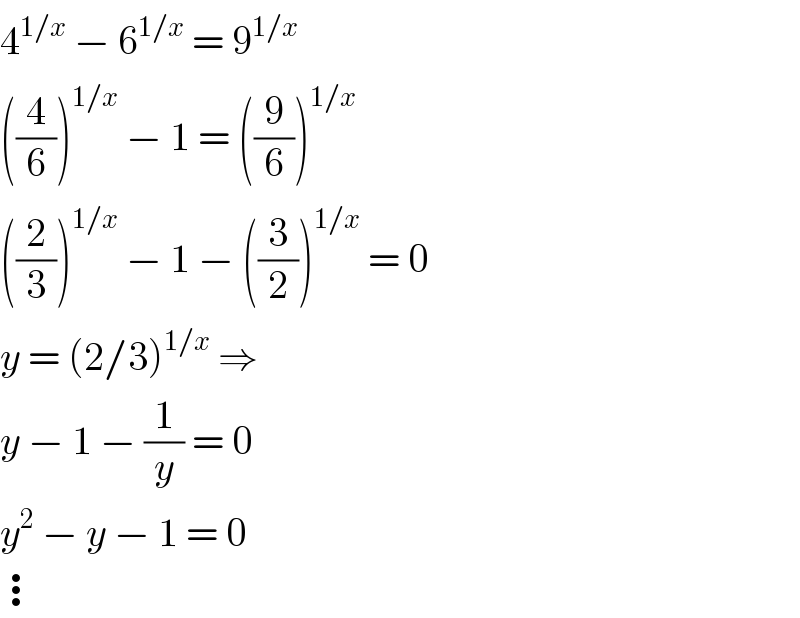
$$\mathrm{4}^{\mathrm{1}/{x}} \:−\:\mathrm{6}^{\mathrm{1}/{x}} \:=\:\mathrm{9}^{\mathrm{1}/{x}} \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{6}}\right)^{\mathrm{1}/{x}} \:−\:\mathrm{1}\:=\:\left(\frac{\mathrm{9}}{\mathrm{6}}\right)^{\mathrm{1}/{x}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}/{x}} \:−\:\mathrm{1}\:−\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{1}/{x}} \:=\:\mathrm{0} \\ $$$${y}\:=\:\left(\mathrm{2}/\mathrm{3}\right)^{\mathrm{1}/{x}} \:\Rightarrow \\ $$$${y}\:−\:\mathrm{1}\:−\:\frac{\mathrm{1}}{{y}}\:=\:\mathrm{0} \\ $$$${y}^{\mathrm{2}} \:−\:{y}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\vdots \\ $$
