Question Number 158306 by mathlove last updated on 02/Nov/21
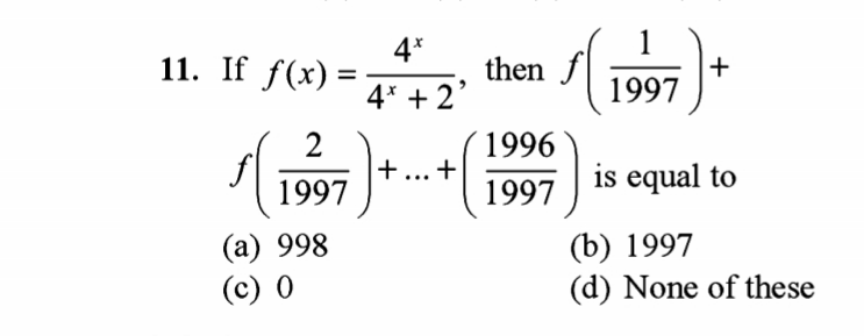
Commented by cortano last updated on 02/Nov/21
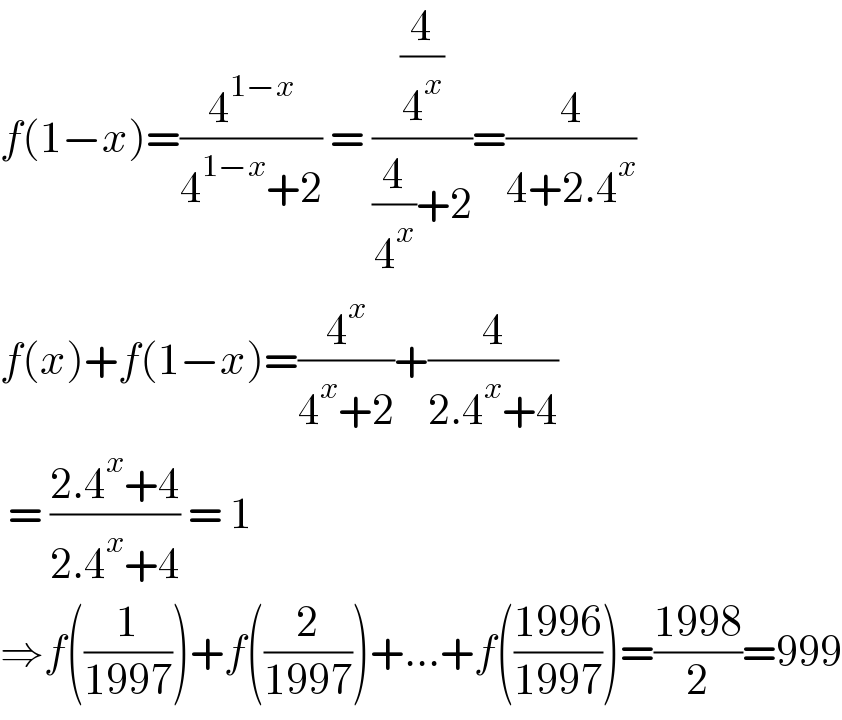
$${f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{4}^{\mathrm{1}−{x}} }{\mathrm{4}^{\mathrm{1}−{x}} +\mathrm{2}}\:=\:\frac{\frac{\mathrm{4}}{\mathrm{4}^{{x}} }}{\frac{\mathrm{4}}{\mathrm{4}^{{x}} }+\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{4}+\mathrm{2}.\mathrm{4}^{{x}} } \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{4}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{2}.\mathrm{4}^{{x}} +\mathrm{4}} \\ $$$$\:=\:\frac{\mathrm{2}.\mathrm{4}^{{x}} +\mathrm{4}}{\mathrm{2}.\mathrm{4}^{{x}} +\mathrm{4}}\:=\:\mathrm{1} \\ $$$$\Rightarrow{f}\left(\frac{\mathrm{1}}{\mathrm{1997}}\right)+{f}\left(\frac{\mathrm{2}}{\mathrm{1997}}\right)+…+{f}\left(\frac{\mathrm{1996}}{\mathrm{1997}}\right)=\frac{\mathrm{1998}}{\mathrm{2}}=\mathrm{999} \\ $$
Commented by mathlove last updated on 02/Nov/21
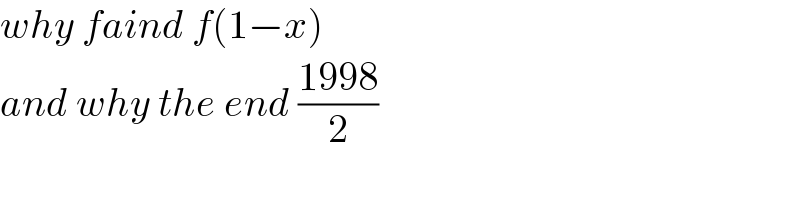
$${why}\:{faind}\:{f}\left(\mathrm{1}−{x}\right) \\ $$$${and}\:{why}\:{the}\:{end}\:\frac{\mathrm{1998}}{\mathrm{2}} \\ $$
Commented by tounghoungko last updated on 03/Nov/21
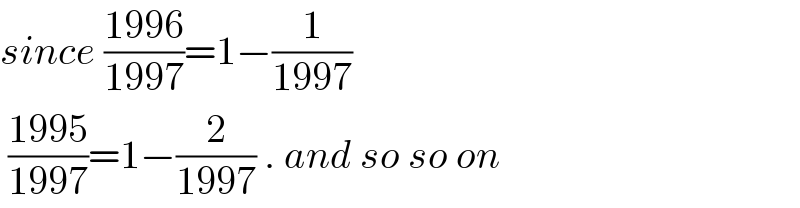
$${since}\:\frac{\mathrm{1996}}{\mathrm{1997}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1997}} \\ $$$$\:\frac{\mathrm{1995}}{\mathrm{1997}}=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1997}}\:.\:{and}\:{so}\:{so}\:{on} \\ $$
