Question Number 158325 by SANOGO last updated on 02/Nov/21

Answered by puissant last updated on 03/Nov/21
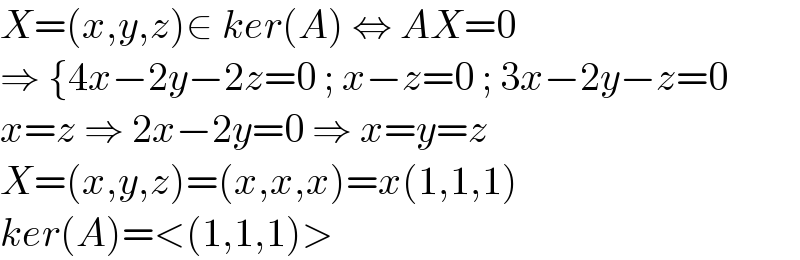
$${X}=\left({x},{y},{z}\right)\in\:{ker}\left({A}\right)\:\Leftrightarrow\:{AX}=\mathrm{0} \\ $$$$\Rightarrow\:\left\{\mathrm{4}{x}−\mathrm{2}{y}−\mathrm{2}{z}=\mathrm{0}\:;\:{x}−{z}=\mathrm{0}\:;\:\mathrm{3}{x}−\mathrm{2}{y}−{z}=\mathrm{0}\right. \\ $$$${x}={z}\:\Rightarrow\:\mathrm{2}{x}−\mathrm{2}{y}=\mathrm{0}\:\Rightarrow\:{x}={y}={z} \\ $$$${X}=\left({x},{y},{z}\right)=\left({x},{x},{x}\right)={x}\left(\mathrm{1},\mathrm{1},\mathrm{1}\right) \\ $$$${ker}\left({A}\right)=<\left(\mathrm{1},\mathrm{1},\mathrm{1}\right)> \\ $$
Answered by puissant last updated on 03/Nov/21
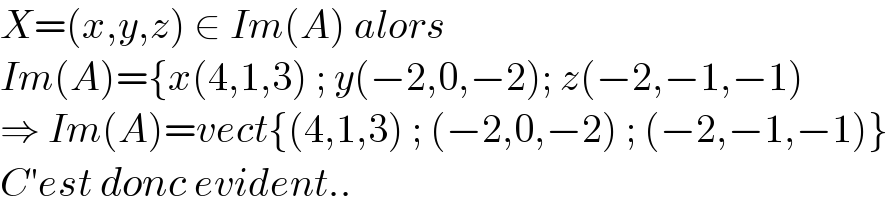
$${X}=\left({x},{y},{z}\right)\:\in\:{Im}\left({A}\right)\:{alors}\: \\ $$$${Im}\left({A}\right)=\left\{{x}\left(\mathrm{4},\mathrm{1},\mathrm{3}\right)\:;\:{y}\left(−\mathrm{2},\mathrm{0},−\mathrm{2}\right);\:{z}\left(−\mathrm{2},−\mathrm{1},−\mathrm{1}\right)\right. \\ $$$$\Rightarrow\:{Im}\left({A}\right)={vect}\left\{\left(\mathrm{4},\mathrm{1},\mathrm{3}\right)\:;\:\left(−\mathrm{2},\mathrm{0},−\mathrm{2}\right)\:;\:\left(−\mathrm{2},−\mathrm{1},−\mathrm{1}\right)\right\} \\ $$$${C}'{est}\:{donc}\:{evident}.. \\ $$
