Question Number 158421 by tebohlouis last updated on 03/Nov/21
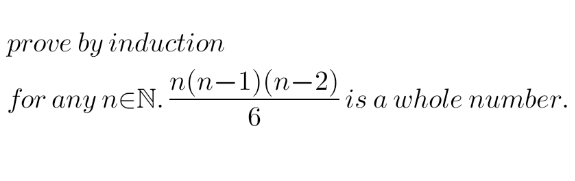
Answered by 1549442205PVT last updated on 04/Nov/21
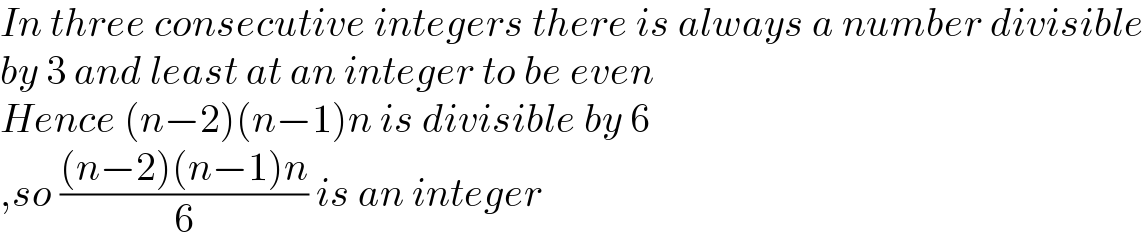
$${In}\:{three}\:{consecutive}\:{integers}\:{there}\:{is}\:{always}\:{a}\:{number}\:{divisible} \\ $$$${by}\:\mathrm{3}\:{and}\:{least}\:{at}\:{an}\:{integer}\:{to}\:{be}\:{even} \\ $$$${Hence}\:\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}\:{is}\:{divisible}\:{by}\:\mathrm{6} \\ $$$$,{so}\:\frac{\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}}{\mathrm{6}}\:{is}\:{an}\:{integer} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Nov/21
![By Induction as required p(n)=((n(n−1)(n−2))/6) case-1: p(1)=0 (a whole number) case-2:Assuming p(k) is whole number. ⇒((k(k−1)(k−2))/6) is whole ⇒((k(k−1)(k−2))/6)+((k(k−1))/2) is whole [∵ One of k & k−1 is certainly even ∴ ((k(k−1))/2) is whole and whole+whole=whole] ⇒((k(k−1)(k−2)+3k(k−1))/6) is whole ⇒((k(k−1)(k−2+3))/6) is whole ⇒((k+1^(−) (k+1^(−) −1)(k+1^(−) −2))/6) is whole ⇒p(k+1) is whole when p(k) is whole ∴ p(n) is true for all natura numbers.](https://www.tinkutara.com/question/Q158432.png)
$$\mathcal{B}{y}\:\mathcal{I}{nduction}\:{as}\:{required} \\ $$$${p}\left({n}\right)=\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{6}} \\ $$$${case}-\mathrm{1}:\:{p}\left(\mathrm{1}\right)=\mathrm{0}\:\left({a}\:{whole}\:{number}\right) \\ $$$${case}-\mathrm{2}:{Assuming}\:{p}\left({k}\right)\:{is}\:{whole}\:{number}. \\ $$$$\Rightarrow\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}}\:{is}\:{whole} \\ $$$$\Rightarrow\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}}+\frac{{k}\left({k}−\mathrm{1}\right)}{\mathrm{2}}\:{is}\:{whole} \\ $$$$\left[\because\:{One}\:{of}\:{k}\:\&\:{k}−\mathrm{1}\:{is}\:{certainly}\:{even}\right. \\ $$$$\:\:\:\therefore\:\frac{{k}\left({k}−\mathrm{1}\right)}{\mathrm{2}}\:{is}\:{whole}\: \\ $$$$\left.\:\:\:\:\:\:\:{and}\:\:{whole}+{whole}={whole}\right] \\ $$$$\Rightarrow\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)+\mathrm{3}{k}\left({k}−\mathrm{1}\right)}{\mathrm{6}}\:{is}\:{whole} \\ $$$$\Rightarrow\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}+\mathrm{3}\right)}{\mathrm{6}}\:{is}\:{whole} \\ $$$$\Rightarrow\frac{\overline {{k}+\mathrm{1}}\:\left(\overline {{k}+\mathrm{1}}−\mathrm{1}\right)\left(\overline {{k}+\mathrm{1}}−\mathrm{2}\right)}{\mathrm{6}}\:{is}\:{whole} \\ $$$$\Rightarrow{p}\left({k}+\mathrm{1}\right)\:{is}\:{whole}\:{when}\:{p}\left({k}\right)\:{is}\:{whole} \\ $$$$\therefore\:{p}\left({n}\right)\:{is}\:{true}\:{for}\:{all}\:{natura}\:{numbers}. \\ $$
