Menu Close

Question-158422

Tinku Tara 0 Comments
Pin




Question Number 158422 by ajfour last updated on 03/Nov/21
Commented by Tawa11 last updated on 04/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 05/Nov/21
Let right bottom angle =(π/4)+2θ (b/c)=((b/(sin ((π/8)+θ)))/((b/(sin ((π/8)+θ)))+b+c)) ⇒(c/b)=1+(1+(c/b))sin α ⇒ (c/b)=((1+sin α)/(1−sin α)) ..(i) similarly (a/c)=((a/(sin ((π/8)−θ)))/(a/(sin ((π/8)−θ)+a+c))) ⇒ (c/a)=((1+sin β)/(1−sin β)) ....(ii) α+β=(π/4) ....(I) tan ((π/4)+2θ)=p ...(iv) c=a+b ...(v) unknowns: θ,p,c,a,b ........................................ work: from (a/c)+(b/c)=1 ((1−sin α)/(1+sin α))+((1−sin β)/(1+sin β))=1 ⇒ 2−2sin αsin β =1+sin α+sin β+sin αsin β ⇒3sin αsin β=1−(sin α+sin β) ⇒(3/2){cos (α−β)−(1/( (√2)))}=1−2sin ((π/8))cos (((α−β)/2)) −−−−−−−−−−−−− let α−β=2δ (3/2)(2cos^2 δ−1−(1/( (√2)))) =1−2sin (π/8)cos δ =1−2λcos δ 6cos^2 δ+4λcos δ−(5+(3/( (√2))))=0 cos δ=−(λ/3)+(√((λ^2 /9)+(((10+3(√2)))/(12)))) cos δ=−((√(2−(√2)))/6)+(√((2−(√2)+30+9(√2))/(36))) 6cos δ=(√(32+8(√2)))−(√(2−(√2))) ⇒ α−β=2δ=2cos^(−1) (k/6) and as α+β=(π/4) p=tan ((π/4)±2θ)=tan ((π/4)±2δ) p=tan ((π/4)±2cos^(−1) (k/6)) −−−−−−−−−−−−− p=tan {(π/4)±2cos^(−1) ((((√(32+8(√2)))−(√(2−(√2))))/6))} −−−−−−−−−−−−−
$${Let}\:{right}\:{bottom}\:{angle} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{4}}+\mathrm{2}\theta \\ $$$$\frac{{b}}{{c}}=\frac{\frac{{b}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}+\theta\right)}}{\frac{{b}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}+\theta\right)}+{b}+{c}} \\ $$$$\Rightarrow\frac{{c}}{{b}}=\mathrm{1}+\left(\mathrm{1}+\frac{{c}}{{b}}\right)\mathrm{sin}\:\alpha\: \\ $$$$\Rightarrow\:\:\frac{{c}}{{b}}=\frac{\mathrm{1}+\mathrm{sin}\:\alpha}{\mathrm{1}−\mathrm{sin}\:\alpha}\:\:\:\:\:\:\:\:..\left({i}\right) \\ $$$$ \\ $$$${similarly} \\ $$$$\frac{{a}}{{c}}=\frac{\frac{{a}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}−\theta\right)}}{\frac{{a}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}−\theta\right)+{a}+{c}}}\: \\ $$$$\Rightarrow\:\:\:\:\:\frac{{c}}{{a}}=\frac{\mathrm{1}+\mathrm{sin}\:\beta}{\mathrm{1}−\mathrm{sin}\:\beta}\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\alpha+\beta=\frac{\pi}{\mathrm{4}}\:\:\:\:\:….\left({I}\right) \\ $$$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{2}\theta\right)={p}\:\:\:\:\:\:\:\:…\left({iv}\right) \\ $$$${c}={a}+{b}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({v}\right) \\ $$$${unknowns}: \\ $$$$\:\:\:\:\theta,{p},{c},{a},{b} \\ $$$$…………………………………. \\ $$$${work}: \\ $$$${from}\:\:\:\:\:\frac{{a}}{{c}}+\frac{{b}}{{c}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}−\mathrm{sin}\:\alpha}{\mathrm{1}+\mathrm{sin}\:\alpha}+\frac{\mathrm{1}−\mathrm{sin}\:\beta}{\mathrm{1}+\mathrm{sin}\:\beta}=\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}−\mathrm{2sin}\:\alpha\mathrm{sin}\:\beta \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta+\mathrm{sin}\:\alpha\mathrm{sin}\:\beta \\ $$$$\Rightarrow\mathrm{3sin}\:\alpha\mathrm{sin}\:\beta=\mathrm{1}−\left(\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta\right) \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}\left\{\mathrm{cos}\:\left(\alpha−\beta\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right\}=\mathrm{1}−\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{8}}\right)\mathrm{cos}\:\left(\frac{\alpha−\beta}{\mathrm{2}}\right) \\ $$$$−−−−−−−−−−−−− \\ $$$${let}\:\:\alpha−\beta=\mathrm{2}\delta \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{2cos}\:^{\mathrm{2}} \delta−\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{2sin}\:\frac{\pi}{\mathrm{8}}\mathrm{cos}\:\delta \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{2}\lambda\mathrm{cos}\:\delta \\ $$$$\mathrm{6cos}\:^{\mathrm{2}} \delta+\mathrm{4}\lambda\mathrm{cos}\:\delta−\left(\mathrm{5}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:\delta=−\frac{\lambda}{\mathrm{3}}+\sqrt{\frac{\lambda^{\mathrm{2}} }{\mathrm{9}}+\frac{\left(\mathrm{10}+\mathrm{3}\sqrt{\mathrm{2}}\right)}{\mathrm{12}}} \\ $$$$\mathrm{cos}\:\delta=−\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{6}}+\sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{2}}+\mathrm{30}+\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{36}}} \\ $$$$\mathrm{6cos}\:\delta=\sqrt{\mathrm{32}+\mathrm{8}\sqrt{\mathrm{2}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\alpha−\beta=\mathrm{2}\delta=\mathrm{2cos}^{−\mathrm{1}} \frac{{k}}{\mathrm{6}} \\ $$$${and}\:{as}\:\:\alpha+\beta=\frac{\pi}{\mathrm{4}}\: \\ $$$${p}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}\pm\mathrm{2}\theta\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}\pm\mathrm{2}\delta\right) \\ $$$${p}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}\pm\mathrm{2cos}^{−\mathrm{1}} \frac{{k}}{\mathrm{6}}\right) \\ $$$$−−−−−−−−−−−−− \\ $$$$\:\boldsymbol{{p}}=\mathrm{tan}\:\left\{\frac{\pi}{\mathrm{4}}\pm\mathrm{2cos}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{32}+\mathrm{8}\sqrt{\mathrm{2}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{6}}\right)\right\} \\ $$$$−−−−−−−−−−−−− \\ $$$$ \\ $$
Commented by mr W last updated on 05/Nov/21
perfect solution!
$${perfect}\:{solution}! \\ $$
Answered by mr W last updated on 04/Nov/21
c+(c/(c−b))(√((c+b)^2 −(c−b)^2 ))=1 ⇒c+((2c(√(bc)))/(c−b))=1 ⇒c+((2c(√(bc)))/a)=1 ...(i) c+(c/(c−a))(√((c+a)^2 −(c−a)^2 ))=p ⇒c+((2c(√(ac)))/(c−a))=p ⇒c+((2c(√(ac)))/b)=p ...(ii) (√(1^2 +p^2 ))=((2c(√(bc)))/a)+((2c(√(ac)))/b) (√(1^2 +p^2 ))=1+p−2c ...(iii) from (iii): c=((1+p−(√(1+p^2 )))/2) from (i): ((√b)/a)=((1−c)/(2c(√c))) from (ii): ((√a)/b)=((p−c)/(2c(√c))) (1/( (√(ab))))=(((1−c)(p−c))/(4c^3 )) ab=((16c^6 )/( (1−c)^2 (p−c)^2 )) ((b/a))^(3/2) =((1−c)/(p−c)) (b/a)=(((1−c)/(p−c)))^(2/3) b^2 =((16c^6 )/( (1−c)^2 (p−c)^2 ))(((1−c)/(p−c)))^(2/3) b=((4c^3 )/( (1−u)(p−u)))(((1−c)/(p−c)))^(1/3) a=((4c^3 )/( (1−c)(p−c)))(((p−c)/(1−c)))^(1/3) a+b=((4c^3 )/( (1−4)(p−c)))[(((1−c)/(p−c)))^(1/3) +(((p−c)/(1−c)))^(1/3) ] c=((4c^3 )/( (1−c)(p−c)))[(((1−c)/(p−c)))^(1/3) +(((p−c)/(1−c)))^(1/3) ] ((4c^2 )/( (1−c)(p−c)))[(((1−c)/(p−c)))^(1/3) +(((p−c)/(1−c)))^(1/3) ]=1 or (1−(2/(1+((√(1+p^2 ))/(p−1)))))^(1/3) +(1−(2/(1−((√(1+p^2 ))/(p−1)))))^(1/3) =((1/(1+p−(√(1+p^2 ))))−(1/2))((p/(1+p−(√(1+p^2 ))))−(1/2)) ⇒p≈0.2970 or 3.3665
$${c}+\frac{{c}}{{c}−{b}}\sqrt{\left({c}+{b}\right)^{\mathrm{2}} −\left({c}−{b}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{c}+\frac{\mathrm{2}{c}\sqrt{{bc}}}{{c}−{b}}=\mathrm{1} \\ $$$$\Rightarrow{c}+\frac{\mathrm{2}{c}\sqrt{{bc}}}{{a}}=\mathrm{1}\:\:\:…\left({i}\right) \\ $$$${c}+\frac{{c}}{{c}−{a}}\sqrt{\left({c}+{a}\right)^{\mathrm{2}} −\left({c}−{a}\right)^{\mathrm{2}} }={p} \\ $$$$\Rightarrow{c}+\frac{\mathrm{2}{c}\sqrt{{ac}}}{{c}−{a}}={p} \\ $$$$\Rightarrow{c}+\frac{\mathrm{2}{c}\sqrt{{ac}}}{{b}}={p}\:\:\:…\left({ii}\right) \\ $$$$\sqrt{\mathrm{1}^{\mathrm{2}} +{p}^{\mathrm{2}} }=\frac{\mathrm{2}{c}\sqrt{{bc}}}{{a}}+\frac{\mathrm{2}{c}\sqrt{{ac}}}{{b}} \\ $$$$\sqrt{\mathrm{1}^{\mathrm{2}} +{p}^{\mathrm{2}} }=\mathrm{1}+{p}−\mathrm{2}{c}\:\:\:…\left({iii}\right) \\ $$$${from}\:\left({iii}\right): \\ $$$${c}=\frac{\mathrm{1}+{p}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${from}\:\left({i}\right): \\ $$$$\frac{\sqrt{{b}}}{{a}}=\frac{\mathrm{1}−{c}}{\mathrm{2}{c}\sqrt{{c}}} \\ $$$${from}\:\left({ii}\right): \\ $$$$\frac{\sqrt{{a}}}{{b}}=\frac{{p}−{c}}{\mathrm{2}{c}\sqrt{{c}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{ab}}}=\frac{\left(\mathrm{1}−{c}\right)\left({p}−{c}\right)}{\mathrm{4}{c}^{\mathrm{3}} } \\ $$$${ab}=\frac{\mathrm{16}{c}^{\mathrm{6}} }{\:\left(\mathrm{1}−{c}\right)^{\mathrm{2}} \left({p}−{c}\right)^{\mathrm{2}} } \\ $$$$\left(\frac{{b}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{1}−{c}}{{p}−{c}} \\ $$$$\frac{{b}}{{a}}=\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{16}{c}^{\mathrm{6}} }{\:\left(\mathrm{1}−{c}\right)^{\mathrm{2}} \left({p}−{c}\right)^{\mathrm{2}} }\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${b}=\frac{\mathrm{4}{c}^{\mathrm{3}} }{\:\left(\mathrm{1}−{u}\right)\left({p}−{u}\right)}\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${a}=\frac{\mathrm{4}{c}^{\mathrm{3}} }{\:\left(\mathrm{1}−{c}\right)\left({p}−{c}\right)}\left(\frac{{p}−{c}}{\mathrm{1}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${a}+{b}=\frac{\mathrm{4}{c}^{\mathrm{3}} }{\:\left(\mathrm{1}−\mathrm{4}\right)\left({p}−{c}\right)}\left[\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\frac{{p}−{c}}{\mathrm{1}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right] \\ $$$${c}=\frac{\mathrm{4}{c}^{\mathrm{3}} }{\:\left(\mathrm{1}−{c}\right)\left({p}−{c}\right)}\left[\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\frac{{p}−{c}}{\mathrm{1}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right] \\ $$$$\frac{\mathrm{4}{c}^{\mathrm{2}} }{\:\left(\mathrm{1}−{c}\right)\left({p}−{c}\right)}\left[\left(\frac{\mathrm{1}−{c}}{{p}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\frac{{p}−{c}}{\mathrm{1}−{c}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right]=\mathrm{1} \\ $$$${or} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}+\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{{p}−\mathrm{1}}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}−\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{{p}−\mathrm{1}}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\left(\frac{\mathrm{1}}{\mathrm{1}+{p}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{{p}}{\mathrm{1}+{p}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{p}\approx\mathrm{0}.\mathrm{2970}\:{or}\:\mathrm{3}.\mathrm{3665} \\ $$
Commented by mr W last updated on 04/Nov/21
an other way: α=(a/c), β=(b/c) tan θ=(p/1)=p=((2tan (θ/2))/(1−tan^2 (θ/2))) tan (θ/2)=(((√(1+p^2 ))−1)/p) sin (θ/2)=((c−b)/(c+b))=((1−β)/(1+β)) β=(2/(1+sin (θ/2)))−1 β=(2/(1+(((√(1+p^2 ))−1)/( (√(2p^2 +2−2(√(1+p^2 ))))))))−1 α=(2/(1+sin ((π/4)−(θ/2))))−1 α=(2/(1+((p+1−(√(1+p^2 )))/( (√2)(√(2p^2 +2−2(√(1+p^2 ))))))))−1 α+β=1 (1/(1+((p+1−(√(1+p^2 )))/( 2(√(p^2 +1−(√(1+p^2 ))))))))+(1/(1+(((√(1+p^2 ))−1)/( (√2)(√(p^2 +1−(√(1+p^2 ))))))))=(3/2)
$${an}\:{other}\:{way}: \\ $$$$\alpha=\frac{{a}}{{c}},\:\beta=\frac{{b}}{{c}} \\ $$$$\mathrm{tan}\:\theta=\frac{{p}}{\mathrm{1}}={p}=\frac{\mathrm{2tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }−\mathrm{1}}{{p}} \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{c}−{b}}{{c}+{b}}=\frac{\mathrm{1}−\beta}{\mathrm{1}+\beta} \\ $$$$\beta=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}−\mathrm{1} \\ $$$$\beta=\frac{\mathrm{2}}{\mathrm{1}+\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }−\mathrm{1}}{\:\sqrt{\mathrm{2}{p}^{\mathrm{2}} +\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}}}−\mathrm{1} \\ $$$$\alpha=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}−\mathrm{1} \\ $$$$\alpha=\frac{\mathrm{2}}{\mathrm{1}+\frac{{p}+\mathrm{1}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}\sqrt{\mathrm{2}{p}^{\mathrm{2}} +\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}}}−\mathrm{1} \\ $$$$\alpha+\beta=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\frac{{p}+\mathrm{1}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{\:\mathrm{2}\sqrt{{p}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}}}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }−\mathrm{1}}{\:\sqrt{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 04/Nov/21
this last blue equation can be solved exactly but the solution is not “nice”
$$\mathrm{this}\:\mathrm{last}\:\mathrm{blue}\:\mathrm{equation}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{exactly} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{not}\:“\mathrm{nice}'' \\ $$
Commented by mr W last updated on 04/Nov/21
wow! i didn′t expect that it can be solved exactly.
$${wow}!\:{i}\:{didn}'{t}\:{expect}\:{that}\:{it}\:{can}\:{be}\:{solved} \\ $$$${exactly}. \\ $$
Commented by MJS_new last updated on 04/Nov/21
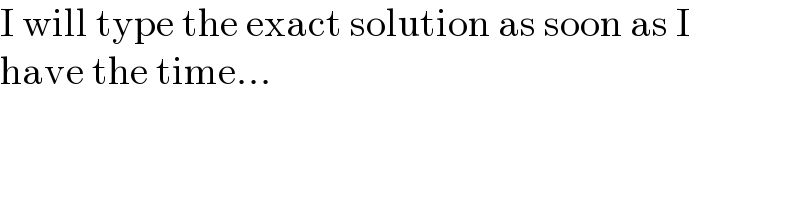
I will type the exact solution as soon as I have the time...
$$\mathrm{I}\:\mathrm{will}\:\mathrm{type}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{as}\:\mathrm{soon}\:\mathrm{as}\:\mathrm{I} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{time}… \\ $$
Commented by MJS_new last updated on 05/Nov/21
let t=p+(√(p^2 +1)) ⇒ p=((t^2 −1)/(2t)); we′re looking for p>0 ⇒ t>1 the blue equation now becomes ((√(t^2 +1))/(1+(√(t^2 +1))))+((2(√(t^2 +1)))/( (√2)(t−1)+2(√(t^2 +1))))=(3/2) this transforms to ((√2)t+2+(√2))(√(t^2 +1))=2t^2 −3(√2)t+2+3(√2) squaring & transforming t^4 +2(1−4(√2))t^3 +(9+8(√2))t^2 −8(3+(√2))t+8(1+(√2))=0 let u=t+(1/2)−2(√2) u^4 −(((81)/2)−20(√2))u^2 +8(17−15(√2))u−((3231)/(16))+127(√2)=0 we can get (u^2 −αu−β)(u^2 +αu−γ)=0 with α=2(√(6−2(√2))) β=((33)/4)−6(√2)+(8−3(√2))(√(3−(√2))) γ=((33)/4)−6(√2)−(8−3(√2))(√(3−(√2))) the real solutions of this are u=(α/2)±((√(α^2 +4β))/2) t=u−(1/2)+2(√2) p=((t^2 −1)/(2t)) I get for p_1 >1 [p_2 =p_1 ^(−1) ] p_1 =−((2−7(√2))/8)−(((2−9(√2))(√(3−(√2))))/(16))+((8−2(√2)−(2−(√2))(√(3−(√2))))/(16))(√(57−32(√2)+4(8−3(√2))(√(3−(√2))))) p_1 ≈3.36651284 p_2 ≈.297043275
$$\mathrm{let}\:{t}={p}+\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\:{p}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}};\:\mathrm{we}'\mathrm{re}\:\mathrm{looking} \\ $$$$\mathrm{for}\:{p}>\mathrm{0}\:\Rightarrow\:{t}>\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{blue}\:\mathrm{equation}\:\mathrm{now}\:\mathrm{becomes} \\ $$$$\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{1}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}+\frac{\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{2}}\left({t}−\mathrm{1}\right)+\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{transforms}\:\mathrm{to} \\ $$$$\left(\sqrt{\mathrm{2}}{t}+\mathrm{2}+\sqrt{\mathrm{2}}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{2}}{t}+\mathrm{2}+\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$$${t}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{1}−\mathrm{4}\sqrt{\mathrm{2}}\right){t}^{\mathrm{3}} +\left(\mathrm{9}+\mathrm{8}\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} −\mathrm{8}\left(\mathrm{3}+\sqrt{\mathrm{2}}\right){t}+\mathrm{8}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{let}\:{u}={t}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${u}^{\mathrm{4}} −\left(\frac{\mathrm{81}}{\mathrm{2}}−\mathrm{20}\sqrt{\mathrm{2}}\right){u}^{\mathrm{2}} +\mathrm{8}\left(\mathrm{17}−\mathrm{15}\sqrt{\mathrm{2}}\right){u}−\frac{\mathrm{3231}}{\mathrm{16}}+\mathrm{127}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{get} \\ $$$$\left({u}^{\mathrm{2}} −\alpha{u}−\beta\right)\left({u}^{\mathrm{2}} +\alpha{u}−\gamma\right)=\mathrm{0} \\ $$$$\mathrm{with} \\ $$$$\alpha=\mathrm{2}\sqrt{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\beta=\frac{\mathrm{33}}{\mathrm{4}}−\mathrm{6}\sqrt{\mathrm{2}}+\left(\mathrm{8}−\mathrm{3}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\sqrt{\mathrm{2}}} \\ $$$$\gamma=\frac{\mathrm{33}}{\mathrm{4}}−\mathrm{6}\sqrt{\mathrm{2}}−\left(\mathrm{8}−\mathrm{3}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\sqrt{\mathrm{2}}} \\ $$$$\mathrm{the}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{this}\:\mathrm{are} \\ $$$${u}=\frac{\alpha}{\mathrm{2}}\pm\frac{\sqrt{\alpha^{\mathrm{2}} +\mathrm{4}\beta}}{\mathrm{2}} \\ $$$${t}={u}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${p}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}} \\ $$$$\mathrm{I}\:\mathrm{get}\:\mathrm{for}\:{p}_{\mathrm{1}} >\mathrm{1}\:\left[{p}_{\mathrm{2}} ={p}_{\mathrm{1}} ^{−\mathrm{1}} \right] \\ $$$${p}_{\mathrm{1}} =−\frac{\mathrm{2}−\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\left(\mathrm{2}−\mathrm{9}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\sqrt{\mathrm{2}}}}{\mathrm{16}}+\frac{\mathrm{8}−\mathrm{2}\sqrt{\mathrm{2}}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\sqrt{\mathrm{2}}}}{\mathrm{16}}\sqrt{\mathrm{57}−\mathrm{32}\sqrt{\mathrm{2}}+\mathrm{4}\left(\mathrm{8}−\mathrm{3}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\sqrt{\mathrm{2}}}} \\ $$$${p}_{\mathrm{1}} \approx\mathrm{3}.\mathrm{36651284} \\ $$$${p}_{\mathrm{2}} \approx.\mathrm{297043275} \\ $$
Commented by mr W last updated on 05/Nov/21
really magic! thanks alot!
$${really}\:{magic}!\:{thanks}\:{alot}! \\ $$
Commented by ajfour last updated on 05/Nov/21
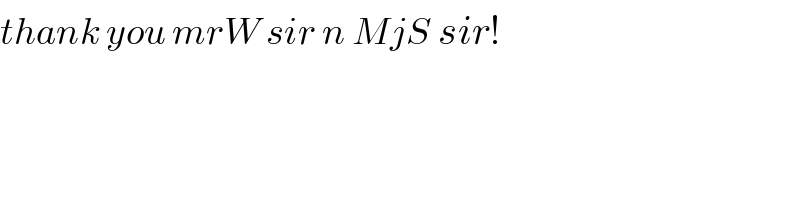
thank you mrW sir n MjS sir!
$${thank}\:{you}\:{mrW}\:{sir}\:{n}\:{MjS}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *