Question Number 158455 by mnjuly1970 last updated on 04/Nov/21

Answered by MJS_new last updated on 05/Nov/21
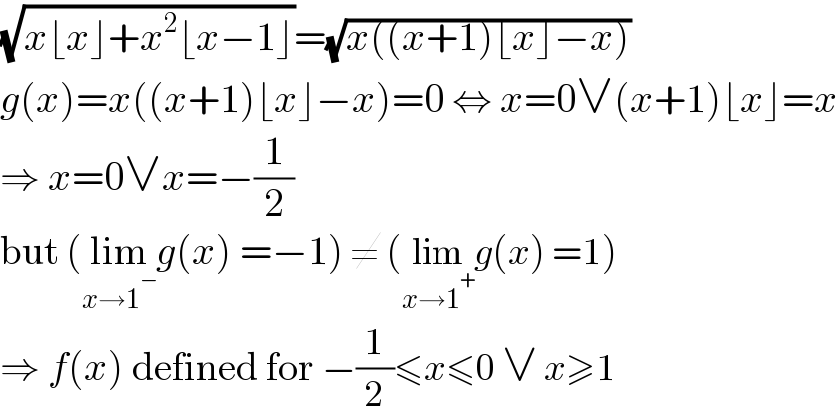
$$\sqrt{{x}\lfloor{x}\rfloor+{x}^{\mathrm{2}} \lfloor{x}−\mathrm{1}\rfloor}=\sqrt{{x}\left(\left({x}+\mathrm{1}\right)\lfloor{x}\rfloor−{x}\right)} \\ $$$${g}\left({x}\right)={x}\left(\left({x}+\mathrm{1}\right)\lfloor{x}\rfloor−{x}\right)=\mathrm{0}\:\Leftrightarrow\:{x}=\mathrm{0}\vee\left({x}+\mathrm{1}\right)\lfloor{x}\rfloor={x} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{but}\:\left(\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}{g}\left({x}\right)\:=−\mathrm{1}\right)\:\neq\:\left(\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{g}\left({x}\right)\:=\mathrm{1}\right) \\ $$$$\Rightarrow\:{f}\left({x}\right)\:\mathrm{defined}\:\mathrm{for}\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\mathrm{0}\:\vee\:{x}\geqslant\mathrm{1} \\ $$
