Question Number 158465 by HongKing last updated on 04/Nov/21

Answered by qaz last updated on 04/Nov/21
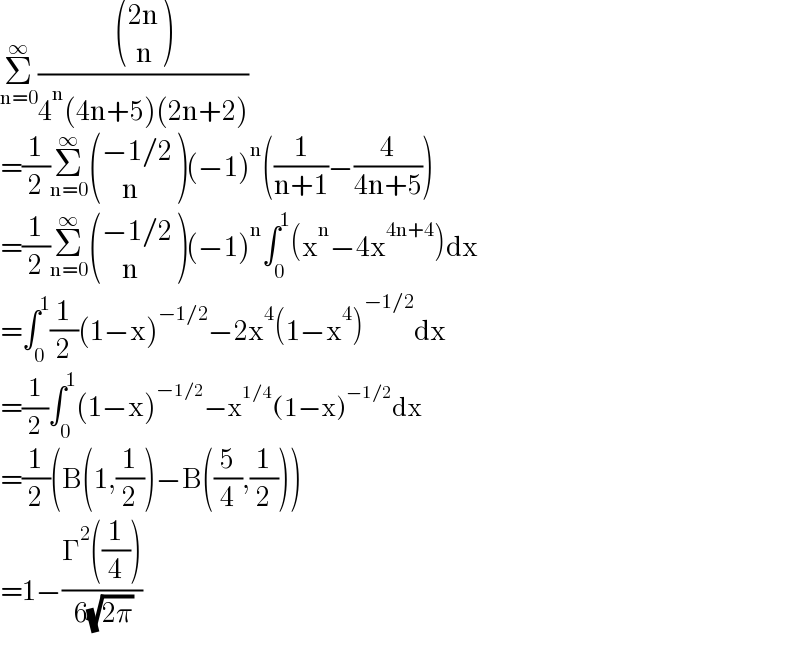
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\begin{pmatrix}{\mathrm{2n}}\\{\:\:\mathrm{n}}\end{pmatrix}}{\mathrm{4}^{\mathrm{n}} \left(\mathrm{4n}+\mathrm{5}\right)\left(\mathrm{2n}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{−\mathrm{1}/\mathrm{2}}\\{\:\:\:\:\:\mathrm{n}}\end{pmatrix}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{4n}+\mathrm{5}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{−\mathrm{1}/\mathrm{2}}\\{\:\:\:\:\:\mathrm{n}}\end{pmatrix}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} −\mathrm{4x}^{\mathrm{4n}+\mathrm{4}} \right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{x}\right)^{−\mathrm{1}/\mathrm{2}} −\mathrm{2x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{4}} \right)^{−\mathrm{1}/\mathrm{2}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{−\mathrm{1}/\mathrm{2}} −\mathrm{x}^{\mathrm{1}/\mathrm{4}} \left(\mathrm{1}−\mathrm{x}\right)^{−\mathrm{1}/\mathrm{2}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{B}\left(\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{B}\left(\frac{\mathrm{5}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\mathrm{1}−\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\:\mathrm{6}\sqrt{\mathrm{2}\pi}} \\ $$
Commented by HongKing last updated on 04/Nov/21
$$\mathrm{cool}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
