Question Number 158472 by ajfour last updated on 04/Nov/21

Commented by ajfour last updated on 05/Nov/21
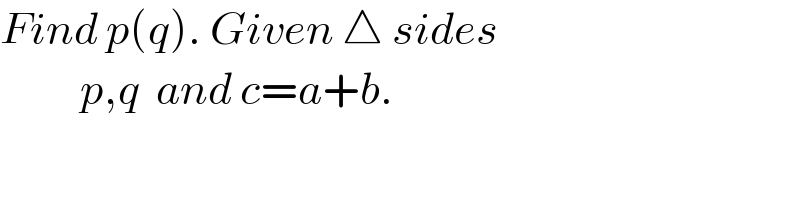
$${Find}\:{p}\left({q}\right).\:{Given}\:\bigtriangleup\:{sides} \\ $$$$\:\:\:\:\:\:\:\:\:\:{p},{q}\:\:{and}\:{c}={a}+{b}. \\ $$
Answered by ajfour last updated on 05/Nov/21
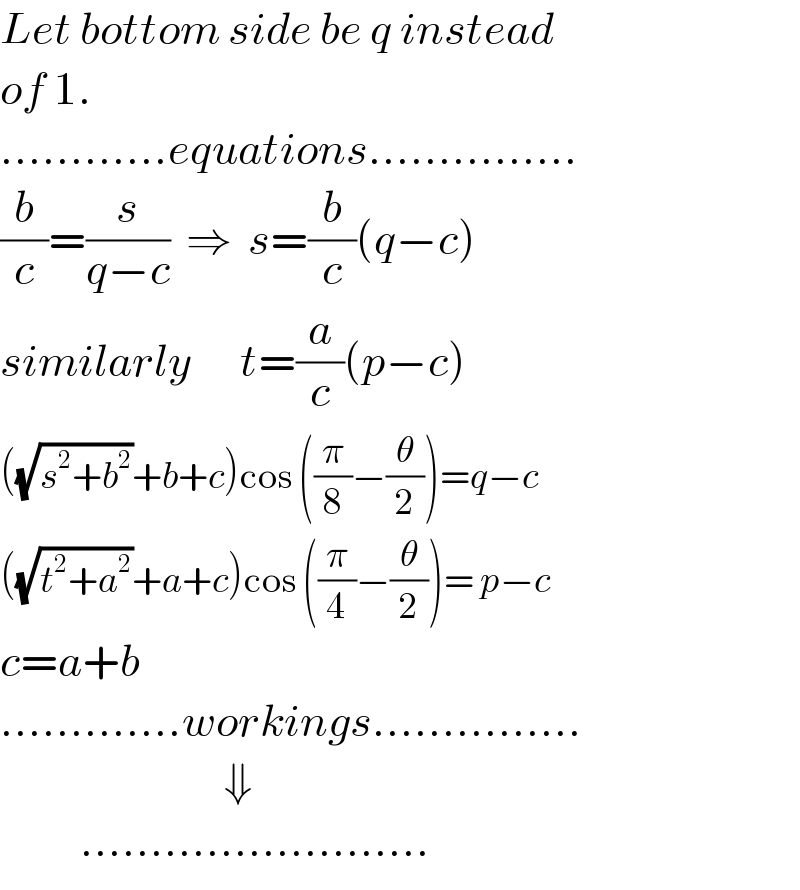
$${Let}\:{bottom}\:{side}\:{be}\:{q}\:{instead} \\ $$$${of}\:\mathrm{1}. \\ $$$$…………{equations}…………… \\ $$$$\frac{{b}}{{c}}=\frac{{s}}{{q}−{c}}\:\:\Rightarrow\:\:{s}=\frac{{b}}{{c}}\left({q}−{c}\right) \\ $$$${similarly}\:\:\:\:\:\:{t}=\frac{{a}}{{c}}\left({p}−{c}\right) \\ $$$$\left(\sqrt{{s}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{b}+{c}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{8}}−\frac{\theta}{\mathrm{2}}\right)={q}−{c} \\ $$$$\left(\sqrt{{t}^{\mathrm{2}} +{a}^{\mathrm{2}} }+{a}+{c}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\:{p}−{c} \\ $$$${c}={a}+{b} \\ $$$$………….{workings}…………… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Downarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:……………………. \\ $$
