Question-158543

Facebook Tweet Pin

Question Number 158543 by ajfour last updated on 06/Nov/21

Commented by ajfour last updated on 06/Nov/21

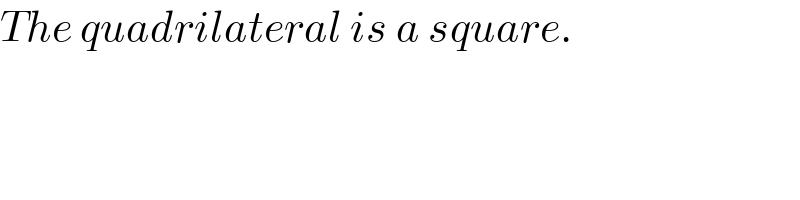
$${The}\:{quadrilateral}\:{is}\:{a}\:{square}. \\ $$

Commented by mr W last updated on 06/Nov/21

Commented by mr W last updated on 06/Nov/21

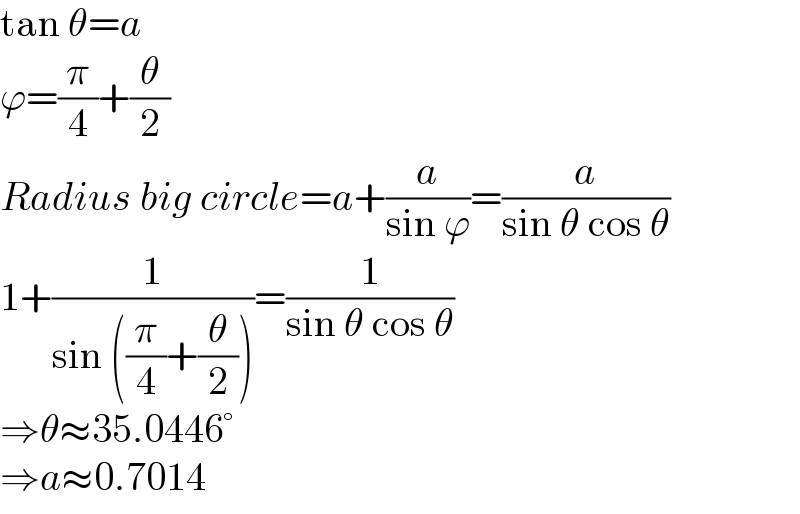
tan θ=a ϕ=(π/4)+(θ/2) Radius big circle=a+(a/(sin ϕ))=(a/(sin θ cos θ)) 1+(1/(sin ((π/4)+(θ/2))))=(1/(sin θ cos θ)) ⇒θ≈35.0446° ⇒a≈0.7014

$$\mathrm{tan}\:\theta={a} \\ $$$$\varphi=\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}} \\ $$$${Radius}\:{big}\:{circle}={a}+\frac{{a}}{\mathrm{sin}\:\varphi}=\frac{{a}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\theta\approx\mathrm{35}.\mathrm{0446}° \\ $$$$\Rightarrow{a}\approx\mathrm{0}.\mathrm{7014} \\ $$

Commented by Tawa11 last updated on 06/Nov/21

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 06/Nov/21

let a=tan θ 1+a^2 =R (R−a)^2 =a^2 +b^2 a^2 +a^4 ={(a^2 +b)sin θ+b}^2 ⇒ (1+a^2 −a)^2 =a^2 +b^2 a^2 +a^4 ={((a(a^2 +b)+b(√(1+a^2 )))/( (√(1+a^2 ))))}^2 a(1+a^2 )=a^3 + (a+(√(1+a^2 )))(1−a)(√(1+a^2 )) ⇒ a((√(1+a^2 ))−a)=(1−a)(√(1+a^2 )) ⇒ (2a−1)(√(1+a^2 ))=a^2 ⇒ (2−(1/a))(√(1+(1/a^2 )))=1 ⇒ a≈0.70136 (>(1/2))

$${let}\:\:{a}=\mathrm{tan}\:\theta \\ $$$$\mathrm{1}+{a}^{\mathrm{2}} ={R} \\ $$$$\left({R}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{a}^{\mathrm{4}} =\left\{\left({a}^{\mathrm{2}} +{b}\right)\mathrm{sin}\:\theta+{b}\right\}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{1}+{a}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{a}^{\mathrm{4}} =\left\{\frac{{a}\left({a}^{\mathrm{2}} +{b}\right)+{b}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\right\}^{\mathrm{2}} \\ $$$${a}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)={a}^{\mathrm{3}} + \\ $$$$\:\:\:\:\:\:\:\left({a}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−{a}\right)\sqrt{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$${a}\left(\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }−{a}\right)=\left(\mathrm{1}−{a}\right)\sqrt{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{a}−\mathrm{1}\right)\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }={a}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}−\frac{\mathrm{1}}{{a}}\right)\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}=\mathrm{1} \\ $$$$\Rightarrow\:\:{a}\approx\mathrm{0}.\mathrm{70136}\:\:\left(>\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply