Question Number 158664 by mr W last updated on 07/Nov/21
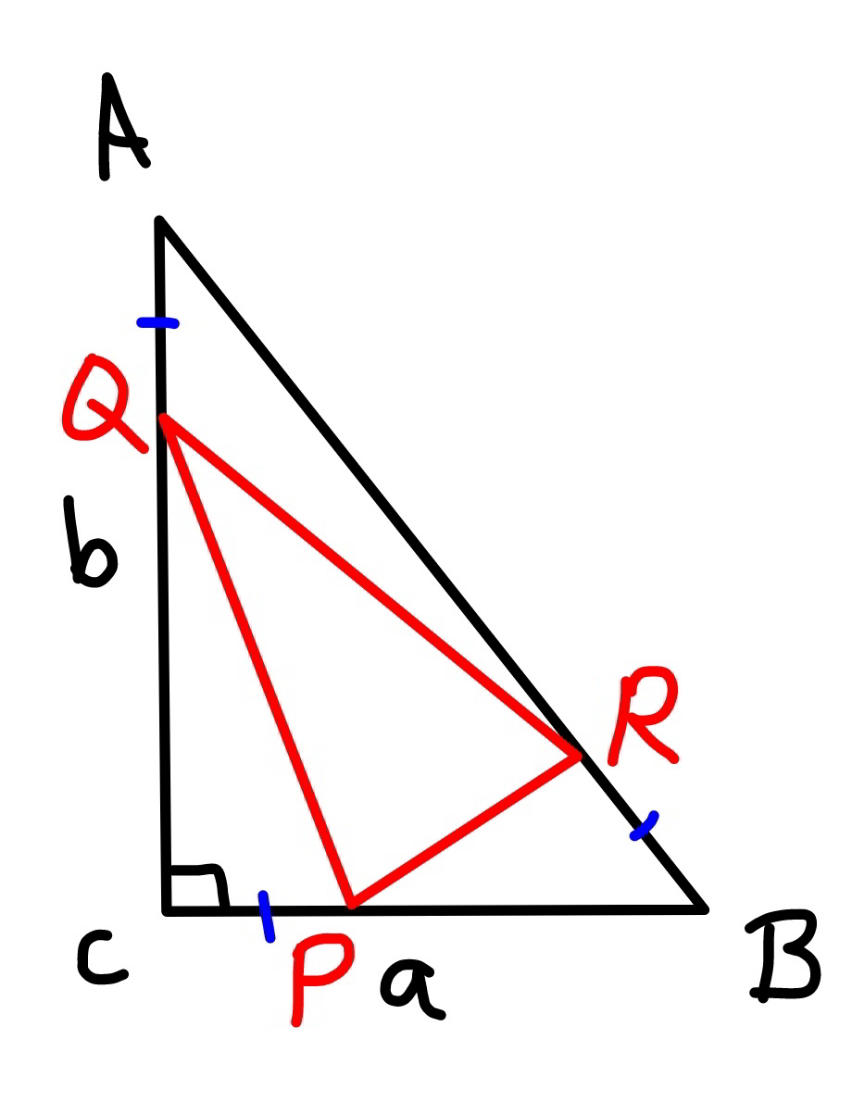
Commented by mr W last updated on 07/Nov/21
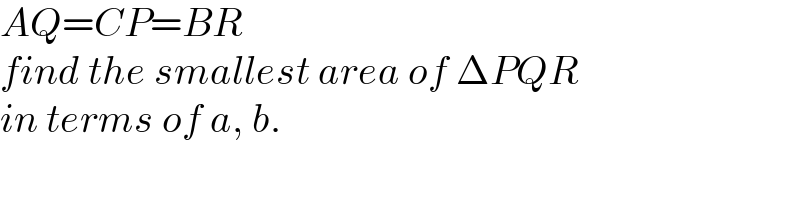
$${AQ}={CP}={BR} \\ $$$${find}\:{the}\:{smallest}\:{area}\:{of}\:\Delta{PQR}\: \\ $$$${in}\:{terms}\:{of}\:{a},\:{b}. \\ $$
Commented by Tawa11 last updated on 07/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 16/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 07/Nov/21
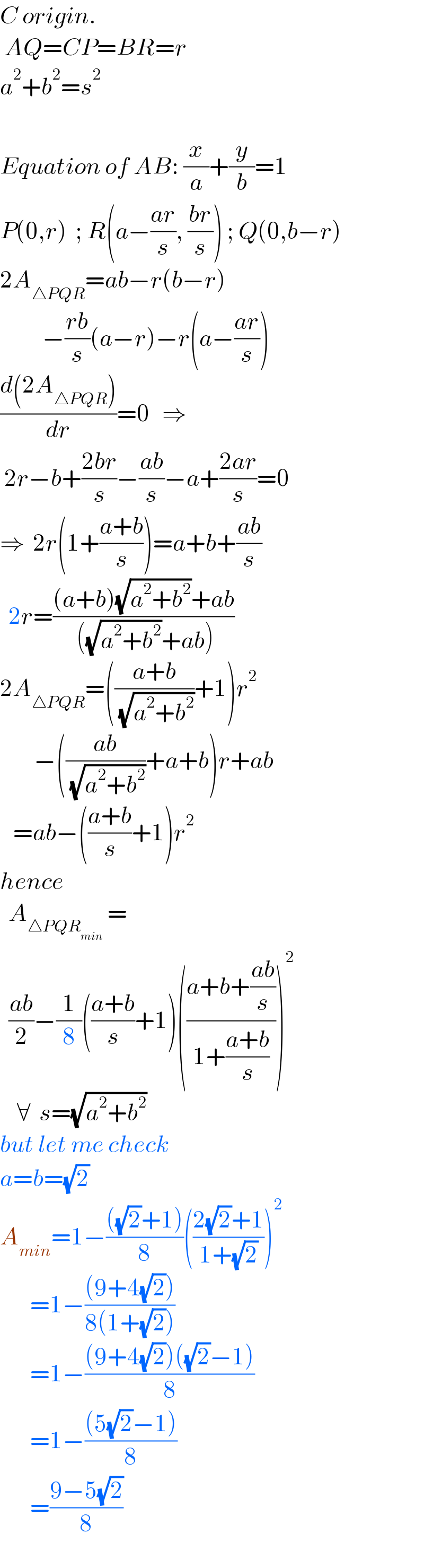
$${C}\:{origin}.\: \\ $$$$\:{AQ}={CP}={BR}={r} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\:\:\:\: \\ $$$${Equation}\:{of}\:{AB}:\:\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1} \\ $$$${P}\left(\mathrm{0},{r}\right)\:\:;\:{R}\left({a}−\frac{{ar}}{{s}},\:\frac{{br}}{{s}}\right)\:;\:{Q}\left(\mathrm{0},{b}−{r}\right) \\ $$$$\mathrm{2}{A}_{\bigtriangleup{PQR}} ={ab}−{r}\left({b}−{r}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{{rb}}{{s}}\left({a}−{r}\right)−{r}\left({a}−\frac{{ar}}{{s}}\right) \\ $$$$\frac{{d}\left(\mathrm{2}{A}_{\bigtriangleup{PQR}} \right)}{{dr}}=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\mathrm{2}{r}−{b}+\frac{\mathrm{2}{br}}{{s}}−\frac{{ab}}{{s}}−{a}+\frac{\mathrm{2}{ar}}{{s}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{r}\left(\mathrm{1}+\frac{{a}+{b}}{{s}}\right)={a}+{b}+\frac{{ab}}{{s}} \\ $$$$\:\:\mathrm{2}{r}=\frac{\left({a}+{b}\right)\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{ab}}{\:\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{ab}\right)} \\ $$$$\mathrm{2}{A}_{\bigtriangleup{PQR}} =\left(\frac{{a}+{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+\mathrm{1}\right){r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:−\left(\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+{a}+{b}\right){r}+{ab} \\ $$$$\:\:\:={ab}−\left(\frac{{a}+{b}}{{s}}+\mathrm{1}\right){r}^{\mathrm{2}} \\ $$$${hence} \\ $$$$\:\:{A}_{\bigtriangleup{PQR}_{{min}} } \:= \\ $$$$\:\:\frac{{ab}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{{a}+{b}}{{s}}+\mathrm{1}\right)\left(\frac{{a}+{b}+\frac{{ab}}{{s}}}{\mathrm{1}+\frac{{a}+{b}}{{s}}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\forall\:\:{s}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${but}\:{let}\:{me}\:{check} \\ $$$${a}={b}=\sqrt{\mathrm{2}} \\ $$$${A}_{{min}} =\mathrm{1}−\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}{\mathrm{8}}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{1}−\frac{\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{2}}\right)}{\mathrm{8}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\:\:\:=\mathrm{1}−\frac{\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{1}−\frac{\left(\mathrm{5}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{9}−\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$
Commented by mr W last updated on 07/Nov/21

$${thanks}\:{sir}! \\ $$$${it}'{s}\:{correct}! \\ $$
Commented by ajfour last updated on 07/Nov/21
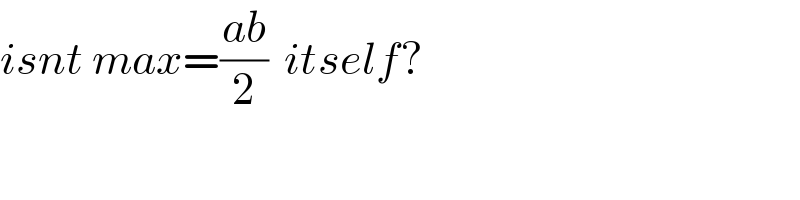
$${isnt}\:{max}=\frac{{ab}}{\mathrm{2}}\:\:{itself}? \\ $$
Commented by mr W last updated on 07/Nov/21

$${yes}! \\ $$
Answered by mr W last updated on 07/Nov/21
![c=(√(a^2 +b^2 )) AQ=BR=CP=t (A_(ΔPQR) /A_(ΔABC) )=1−((t(b−t))/(ab))−((t(a−t))/(ac))−((t(c−t))/(bc)) (A_(ΔPQR) /A_(ΔABC) )=1−((t(ab+bc+ca)−t^2 (a+b+c))/(abc)) such that A_(ΔPQR) is minimum: (d/dt)((A_(ΔPQR) /A_(ΔABC) ))=0 ⇒(ab+bc+ca)−2(a+b+c)t=0 ⇒t=((ab+bc+ca)/(2(a+b+c))) ((max. A_(ΔPQR) )/A_(ΔABC) )=1−(((ab+bc+ca)^2 )/(4abc(a+b+c))) max. A_(ΔPQR) =((ab)/2)−(([ab+(a+b)(√(a^2 +b^2 ))]^2 )/(8(√(a^2 +b^2 ))(a+b+(√(a^2 +b^2 )))))](https://www.tinkutara.com/question/Q158667.png)
$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${AQ}={BR}={CP}={t} \\ $$$$\frac{{A}_{\Delta{PQR}} }{{A}_{\Delta{ABC}} }=\mathrm{1}−\frac{{t}\left({b}−{t}\right)}{{ab}}−\frac{{t}\left({a}−{t}\right)}{{ac}}−\frac{{t}\left({c}−{t}\right)}{{bc}} \\ $$$$\frac{{A}_{\Delta{PQR}} }{{A}_{\Delta{ABC}} }=\mathrm{1}−\frac{{t}\left({ab}+{bc}+{ca}\right)−{t}^{\mathrm{2}} \left({a}+{b}+{c}\right)}{{abc}} \\ $$$${such}\:{that}\:{A}_{\Delta{PQR}} \:{is}\:{minimum}:\: \\ $$$$\:\frac{{d}}{{dt}}\left(\frac{{A}_{\Delta{PQR}} }{{A}_{\Delta{ABC}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\left({ab}+{bc}+{ca}\right)−\mathrm{2}\left({a}+{b}+{c}\right){t}=\mathrm{0}\: \\ $$$$\Rightarrow{t}=\frac{{ab}+{bc}+{ca}}{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\frac{{max}.\:{A}_{\Delta{PQR}} }{{A}_{\Delta{ABC}} }=\mathrm{1}−\frac{\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} }{\mathrm{4}{abc}\left({a}+{b}+{c}\right)} \\ $$$${max}.\:{A}_{\Delta{PQR}} =\frac{{ab}}{\mathrm{2}}−\frac{\left[{ab}+\left({a}+{b}\right)\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right]^{\mathrm{2}} }{\mathrm{8}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)} \\ $$
