Question Number 158674 by cortano last updated on 07/Nov/21

Commented by tounghoungko last updated on 07/Nov/21
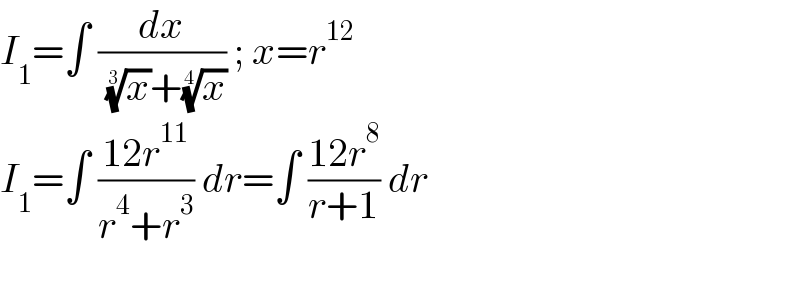
$${I}_{\mathrm{1}} =\int\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{4}}]{{x}}}\:;\:{x}={r}^{\mathrm{12}} \\ $$$${I}_{\mathrm{1}} =\int\:\frac{\mathrm{12}{r}^{\mathrm{11}} }{{r}^{\mathrm{4}} +{r}^{\mathrm{3}} }\:{dr}=\int\:\frac{\mathrm{12}{r}^{\mathrm{8}} }{{r}+\mathrm{1}}\:{dr} \\ $$$$ \\ $$
Commented by tounghoungko last updated on 07/Nov/21
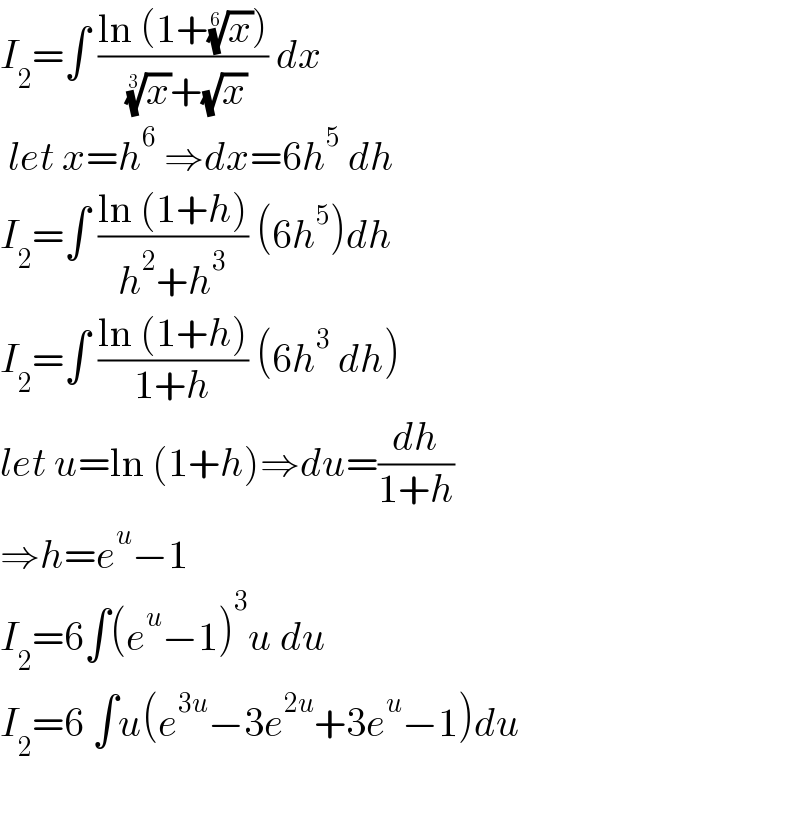
$${I}_{\mathrm{2}} =\int\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}\right)}{\:\sqrt[{\mathrm{3}}]{{x}}+\sqrt{{x}}}\:{dx} \\ $$$$\:{let}\:{x}={h}^{\mathrm{6}} \:\Rightarrow{dx}=\mathrm{6}{h}^{\mathrm{5}} \:{dh} \\ $$$${I}_{\mathrm{2}} =\int\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{h}\right)}{{h}^{\mathrm{2}} +{h}^{\mathrm{3}} }\:\left(\mathrm{6}{h}^{\mathrm{5}} \right){dh} \\ $$$${I}_{\mathrm{2}} =\int\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{h}\right)}{\mathrm{1}+{h}}\:\left(\mathrm{6}{h}^{\mathrm{3}} \:{dh}\right) \\ $$$${let}\:{u}=\mathrm{ln}\:\left(\mathrm{1}+{h}\right)\Rightarrow{du}=\frac{{dh}}{\mathrm{1}+{h}} \\ $$$$\Rightarrow{h}={e}^{{u}} −\mathrm{1} \\ $$$${I}_{\mathrm{2}} =\mathrm{6}\int\left({e}^{{u}} −\mathrm{1}\right)^{\mathrm{3}} {u}\:{du} \\ $$$${I}_{\mathrm{2}} =\mathrm{6}\:\int{u}\left({e}^{\mathrm{3}{u}} −\mathrm{3}{e}^{\mathrm{2}{u}} +\mathrm{3}{e}^{{u}} −\mathrm{1}\right){du} \\ $$$$\: \\ $$
