Question Number 158708 by ajfour last updated on 07/Nov/21
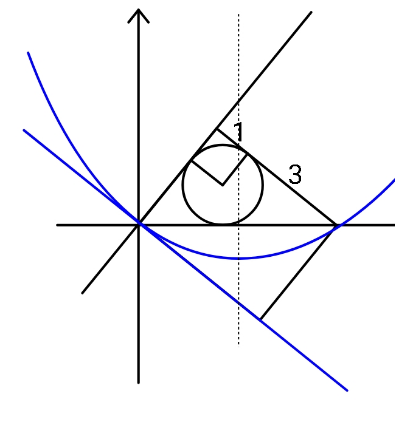
Commented by ajfour last updated on 07/Nov/21
$${Find}\:{equation}\:{of}\:{parabola}. \\ $$
Answered by mr W last updated on 08/Nov/21
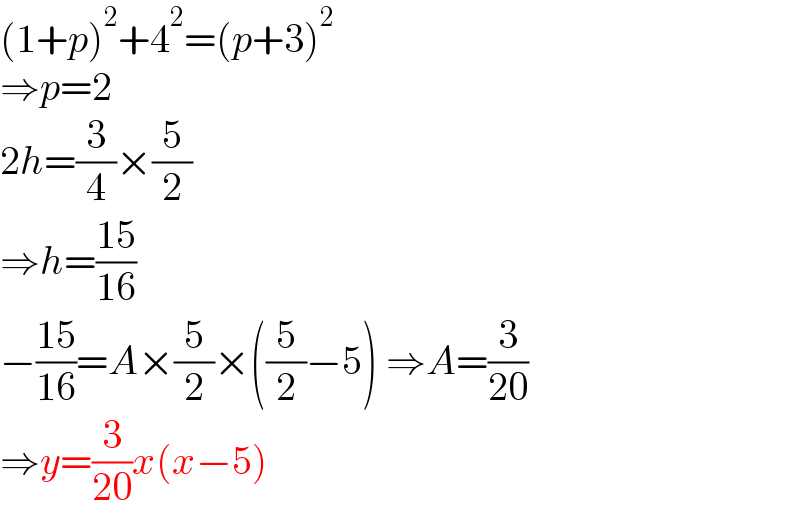
$$\left(\mathrm{1}+{p}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} =\left({p}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{p}=\mathrm{2} \\ $$$$\mathrm{2}{h}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{h}=\frac{\mathrm{15}}{\mathrm{16}} \\ $$$$−\frac{\mathrm{15}}{\mathrm{16}}={A}×\frac{\mathrm{5}}{\mathrm{2}}×\left(\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{5}\right)\:\Rightarrow{A}=\frac{\mathrm{3}}{\mathrm{20}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{3}}{\mathrm{20}}{x}\left({x}−\mathrm{5}\right) \\ $$
Commented by mr W last updated on 08/Nov/21
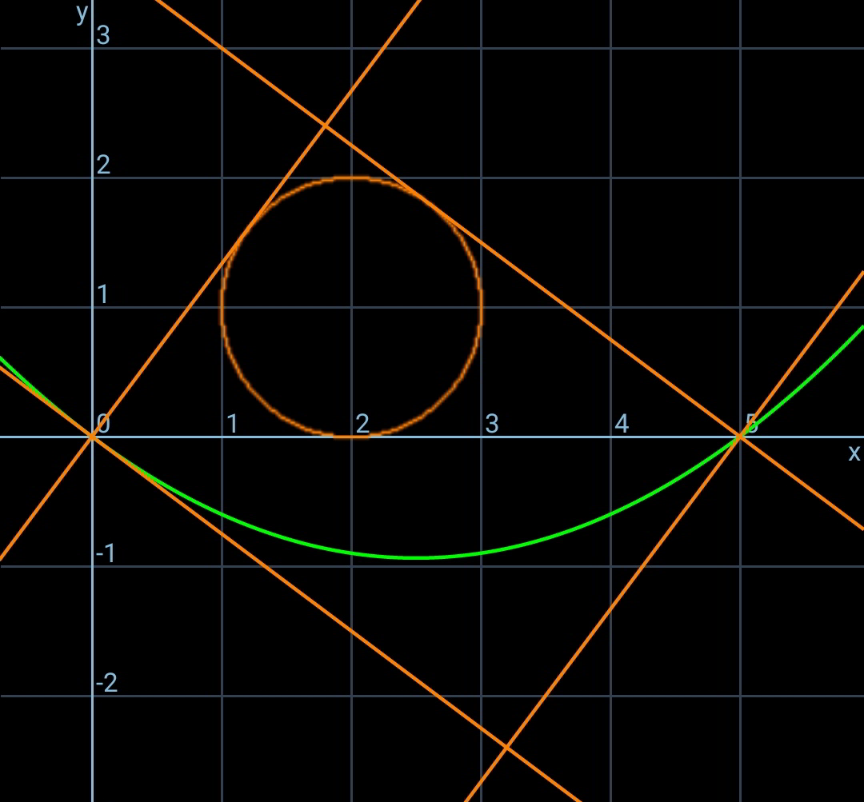
Commented by mr W last updated on 08/Nov/21
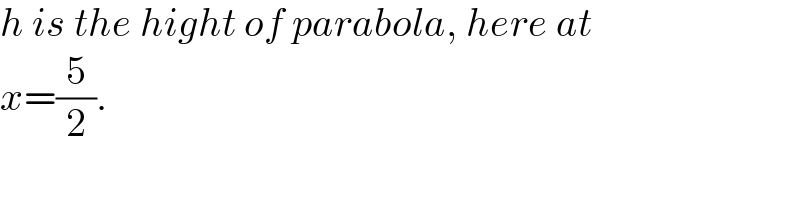
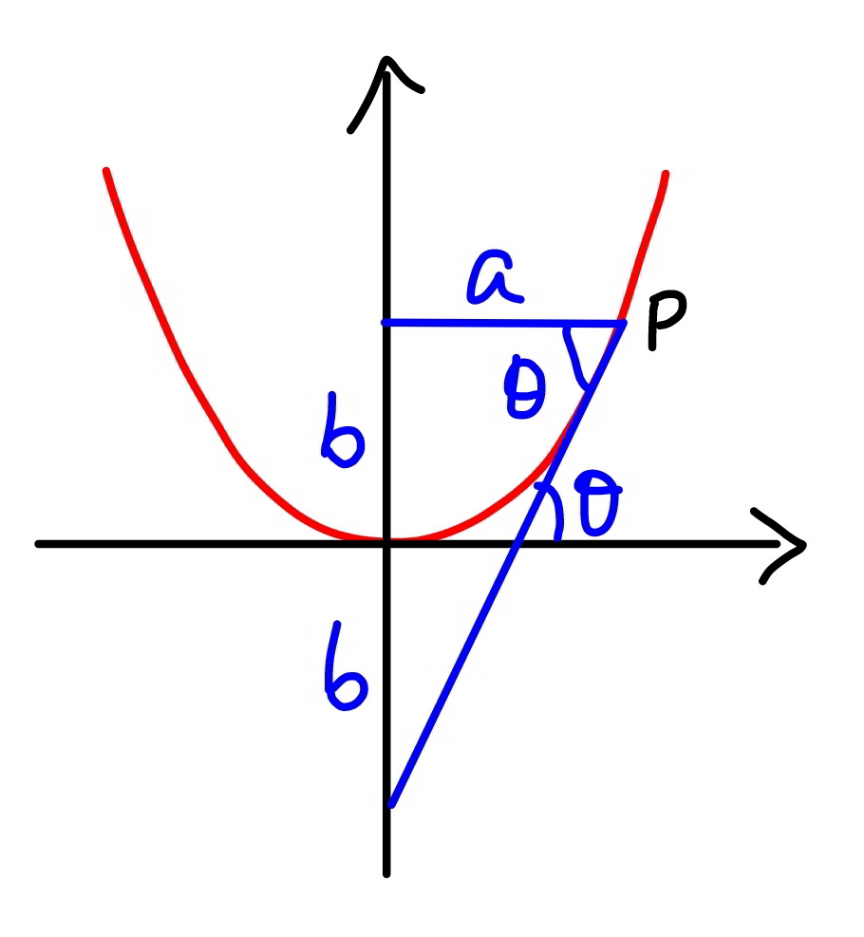
$${h}\:{is}\:{the}\:{hight}\:{of}\:{parabola},\:{here}\:{at} \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{2}}. \\ $$
Commented by ajfour last updated on 08/Nov/21

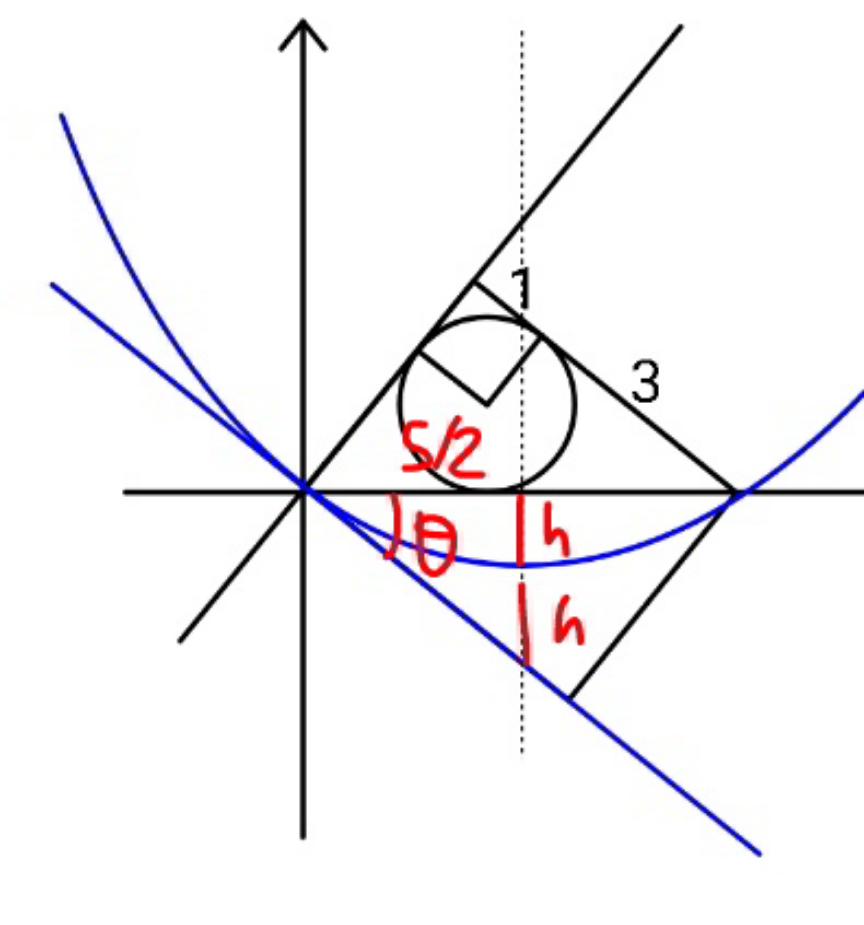
$$\mathrm{2}{h}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{2}}\:\:\:\:\:\:\left({how}?\right) \\ $$$$ \\ $$
Commented by mr W last updated on 08/Nov/21
Commented by ajfour last updated on 08/Nov/21
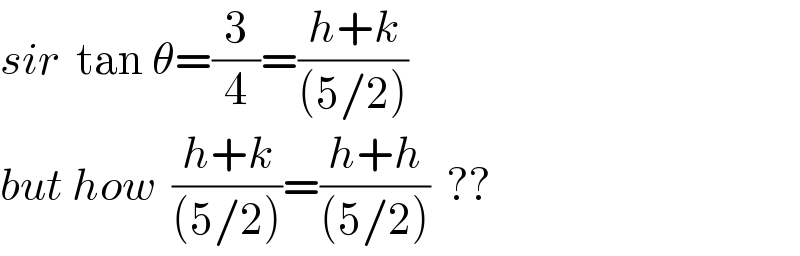
$${sir}\:\:\mathrm{tan}\:\theta=\frac{\mathrm{3}}{\mathrm{4}}=\frac{{h}+{k}}{\left(\mathrm{5}/\mathrm{2}\right)} \\ $$$${but}\:{how}\:\:\frac{{h}+{k}}{\left(\mathrm{5}/\mathrm{2}\right)}=\frac{{h}+{h}}{\left(\mathrm{5}/\mathrm{2}\right)}\:\:?? \\ $$
Commented by mr W last updated on 08/Nov/21
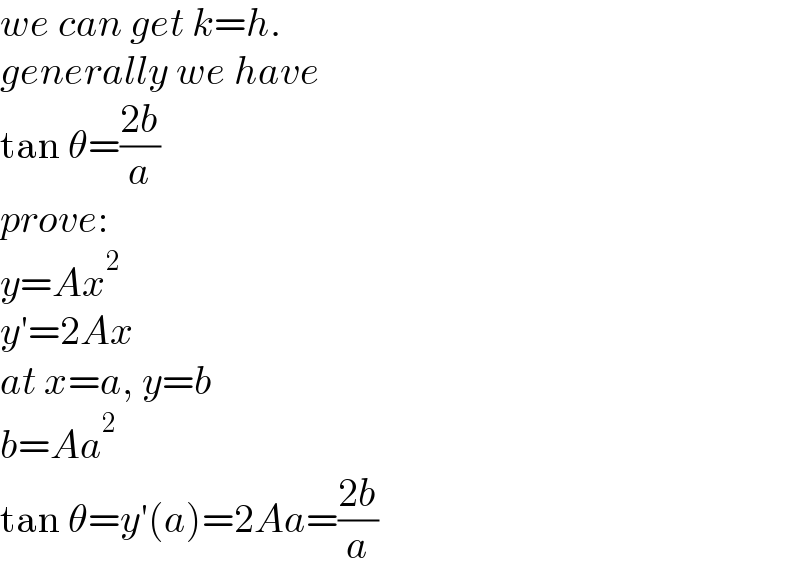
$${we}\:{can}\:{get}\:{k}={h}. \\ $$$${generally}\:{we}\:{have} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}{b}}{{a}} \\ $$$${prove}: \\ $$$${y}={Ax}^{\mathrm{2}} \\ $$$${y}'=\mathrm{2}{Ax} \\ $$$${at}\:{x}={a},\:{y}={b} \\ $$$${b}={Aa}^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta={y}'\left({a}\right)=\mathrm{2}{Aa}=\frac{\mathrm{2}{b}}{{a}} \\ $$
Commented by mr W last updated on 08/Nov/21
Commented by ajfour last updated on 08/Nov/21
$${Excellent},\:{thank}\:{you}\:{sir}. \\ $$
Answered by ajfour last updated on 08/Nov/21
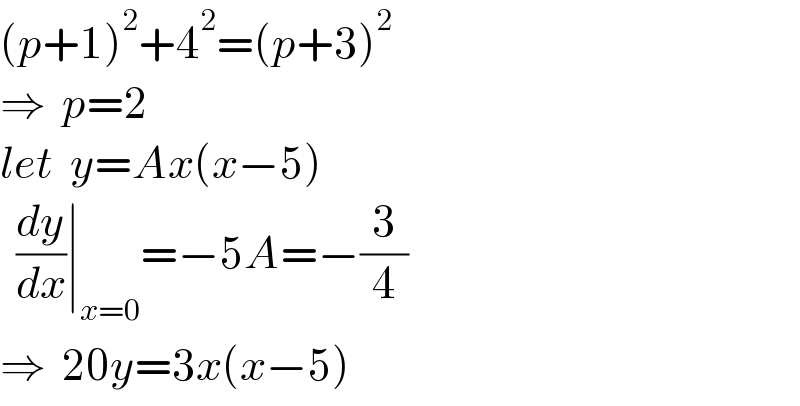
$$\left({p}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} =\left({p}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{p}=\mathrm{2} \\ $$$${let}\:\:{y}={Ax}\left({x}−\mathrm{5}\right) \\ $$$$\:\:\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{0}} =−\mathrm{5}{A}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\mathrm{20}{y}=\mathrm{3}{x}\left({x}−\mathrm{5}\right) \\ $$
