Question Number 158740 by ajfour last updated on 08/Nov/21
Commented by ajfour last updated on 08/Nov/21
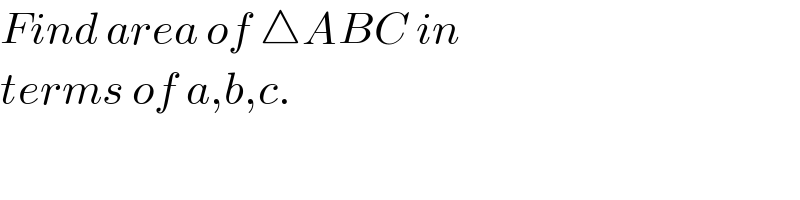
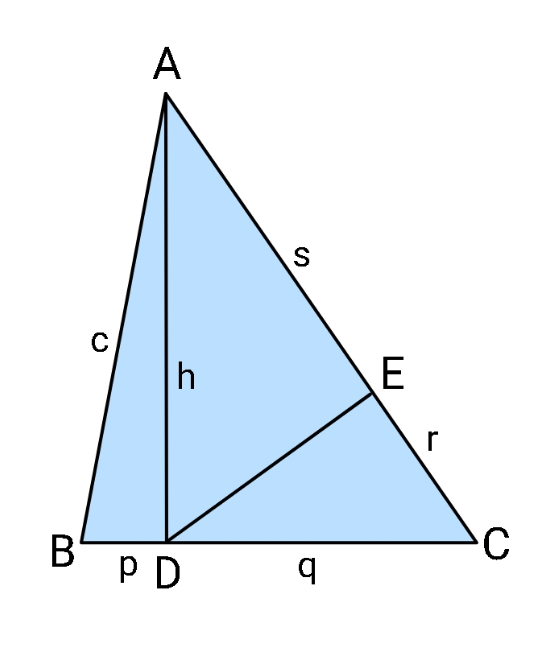
$${Find}\:{area}\:{of}\:\bigtriangleup{ABC}\:{in} \\ $$$${terms}\:{of}\:{a},{b},{c}. \\ $$
Answered by ajfour last updated on 08/Nov/21
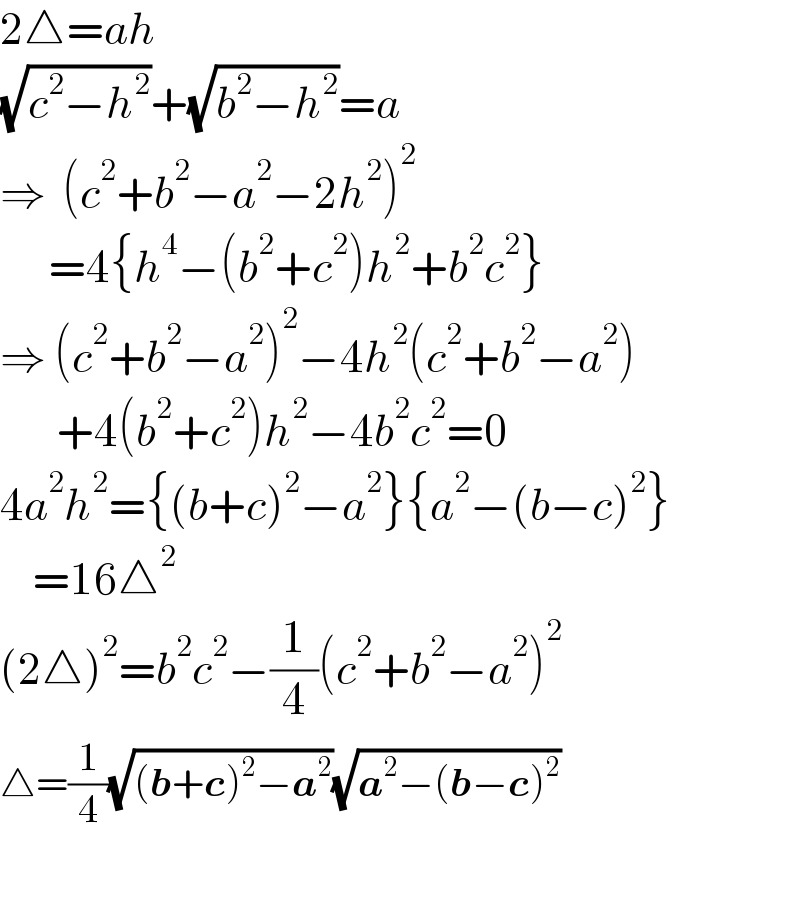
$$\mathrm{2}\bigtriangleup={ah} \\ $$$$\sqrt{{c}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }={a} \\ $$$$\Rightarrow\:\:\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{2}{h}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\mathrm{4}\left\{{h}^{\mathrm{4}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){h}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right\} \\ $$$$\Rightarrow\:\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} \left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:+\mathrm{4}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){h}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} =\left\{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:=\mathrm{16}\bigtriangleup^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\bigtriangleup\right)^{\mathrm{2}} ={b}^{\mathrm{2}} {c}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\left(\boldsymbol{{b}}−\boldsymbol{{c}}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by mr W last updated on 08/Nov/21
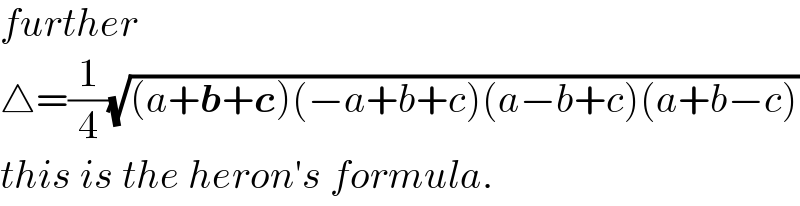
$${further} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({a}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$${this}\:{is}\:{the}\:{heron}'{s}\:{formula}. \\ $$
