Question Number 158780 by EbrimaDanjo last updated on 08/Nov/21

Answered by puissant last updated on 08/Nov/21
![K=∫_0 ^1 e^e^e^e^e^x e^e^e^e^x e^e^e^x e^e^x e^x dx ; u=e^x → x=lnu → dx=(du/u) ⇒ K=∫_1 ^e e^e^e^e^u e^e^e^u e^e^u e^u du ; v=e^u → u=lnv → du=(dv/v) ⇒ K=∫_e ^e^e e^e^e^v e^e^v e^v dv ; w=e^v → v=lnw → dv=(dw/w) ⇒ K=∫_e^e ^e^e^e e^e^w e^w dw ; t=e^w → w=lnt → dw=(dt/t) ⇒ K= ∫_e^e^e ^e^e^e^e e^t dt = [e^t ]_e^e^e ^e^e^e^e = e^e^e^e^e −e^e^e^e ∴∵ K = e^e^e^e^e −e^e^e^e ...■ .................Le puissant.................](https://www.tinkutara.com/question/Q158784.png)
$${K}=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{e}^{{e}^{{e}^{{e}^{{x}} } } } } {e}^{{e}^{{e}^{{e}^{{x}} } } } {e}^{{e}^{{e}^{{x}} } } {e}^{{e}^{{x}} } {e}^{{x}} {dx}\:;\:{u}={e}^{{x}} \:\rightarrow\:{x}={lnu}\:\rightarrow\:{dx}=\frac{{du}}{{u}} \\ $$$$\Rightarrow\:{K}=\int_{\mathrm{1}} ^{{e}} {e}^{{e}^{{e}^{{e}^{{u}} } } } {e}^{{e}^{{e}^{{u}} } } {e}^{{e}^{{u}} } {e}^{{u}} {du}\:;\:{v}={e}^{{u}} \rightarrow\:{u}={lnv}\:\rightarrow\:{du}=\frac{{dv}}{{v}} \\ $$$$\Rightarrow\:{K}=\int_{{e}} ^{{e}^{{e}} } {e}^{{e}^{{e}^{{v}} } } {e}^{{e}^{{v}} } {e}^{{v}} {dv}\:;\:{w}={e}^{{v}} \:\rightarrow\:{v}={lnw}\:\rightarrow\:{dv}=\frac{{dw}}{{w}} \\ $$$$\Rightarrow\:{K}=\int_{{e}^{{e}} } ^{{e}^{{e}^{{e}} } } {e}^{{e}^{{w}} } {e}^{{w}} {dw}\:;\:{t}={e}^{{w}} \:\rightarrow\:{w}={lnt}\:\rightarrow\:{dw}=\frac{{dt}}{{t}} \\ $$$$\Rightarrow\:{K}=\:\int_{{e}^{{e}^{{e}} } } ^{{e}^{{e}^{{e}^{{e}} } } } {e}^{{t}} {dt}\:=\:\left[{e}^{{t}} \right]_{{e}^{{e}^{{e}} } } ^{{e}^{{e}^{{e}^{{e}} } } } =\:{e}^{{e}^{{e}^{{e}^{{e}} } } } −{e}^{{e}^{{e}^{{e}} } } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:\:\:{K}\:=\:{e}^{{e}^{{e}^{{e}^{{e}} } } } −{e}^{{e}^{{e}^{{e}} } } …\blacksquare \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……………..\mathscr{L}{e}\:{puissant}…………….. \\ $$
Answered by MJS_new last updated on 08/Nov/21
![let e_1 (x) =e^x ; e_2 (x) =e^e^x ... (d/dx)[e_n (x)]=Π_(j=1) ^n e_j (x) ⇒ ∫e_5 (x) e_4 (x) e_3 (x) e_2 (x) e_1 (x)dx= =e_5 (x)+C ⇒ answer is e_5 (1)−e_5 (0)=e_5 (1)−e_4 (1)](https://www.tinkutara.com/question/Q158788.png)
$$\mathrm{let}\:\mathrm{e}_{\mathrm{1}} \left({x}\right)\:=\mathrm{e}^{{x}} ;\:\mathrm{e}_{\mathrm{2}} \left({x}\right)\:=\mathrm{e}^{\mathrm{e}^{{x}} } … \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{e}_{{n}} \left({x}\right)\right]=\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{e}_{{j}} \left({x}\right) \\ $$$$\Rightarrow \\ $$$$\int\mathrm{e}_{\mathrm{5}} \left({x}\right)\:\mathrm{e}_{\mathrm{4}} \left({x}\right)\:\mathrm{e}_{\mathrm{3}} \left({x}\right)\:\mathrm{e}_{\mathrm{2}} \left({x}\right)\:\mathrm{e}_{\mathrm{1}} \left({x}\right)\mathrm{dx}= \\ $$$$=\mathrm{e}_{\mathrm{5}} \left({x}\right)+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{e}_{\mathrm{5}} \left(\mathrm{1}\right)−\mathrm{e}_{\mathrm{5}} \left(\mathrm{0}\right)=\mathrm{e}_{\mathrm{5}} \left(\mathrm{1}\right)−\mathrm{e}_{\mathrm{4}} \left(\mathrm{1}\right) \\ $$
Commented by MJS_new last updated on 08/Nov/21
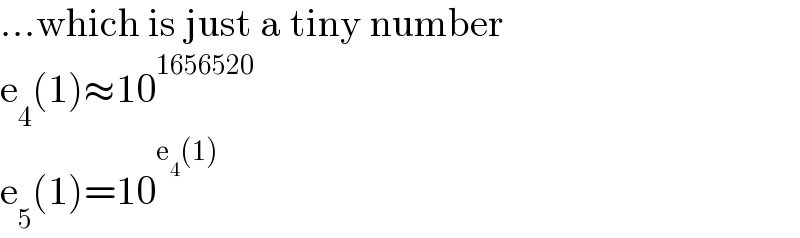
$$…\mathrm{which}\:\mathrm{is}\:\mathrm{just}\:\mathrm{a}\:\mathrm{tiny}\:\mathrm{number} \\ $$$$\mathrm{e}_{\mathrm{4}} \left(\mathrm{1}\right)\approx\mathrm{10}^{\mathrm{1656520}} \\ $$$$\mathrm{e}_{\mathrm{5}} \left(\mathrm{1}\right)=\mathrm{10}^{\mathrm{e}_{\mathrm{4}} \left(\mathrm{1}\right)} \\ $$
Commented by EbrimaDanjo last updated on 08/Nov/21
$$\mathrm{wow}\:\mathrm{well}\:\mathrm{done}\:\mathrm{sir} \\ $$
