Question Number 158847 by mathlove last updated on 09/Nov/21

Answered by mr W last updated on 09/Nov/21
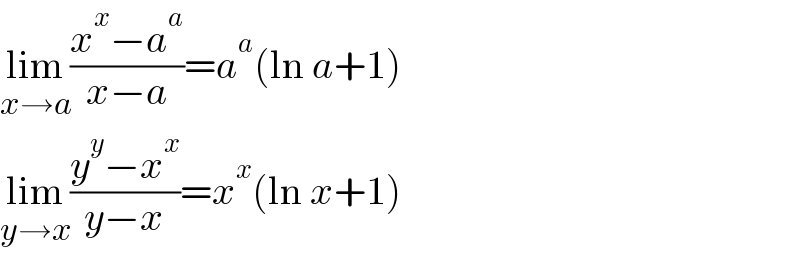
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{x}} −{a}^{{a}} }{{x}−{a}}={a}^{{a}} \left(\mathrm{ln}\:{a}+\mathrm{1}\right) \\ $$$$\underset{{y}\rightarrow{x}} {\mathrm{lim}}\frac{{y}^{{y}} −{x}^{{x}} }{{y}−{x}}={x}^{{x}} \left(\mathrm{ln}\:{x}+\mathrm{1}\right) \\ $$
Commented by mathlove last updated on 09/Nov/21

$${solution}? \\ $$
Commented by mr W last updated on 09/Nov/21
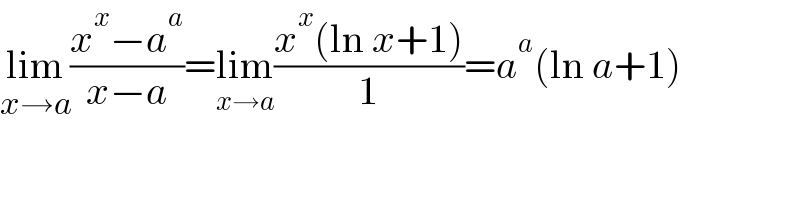
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{x}} −{a}^{{a}} }{{x}−{a}}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{x}} \left(\mathrm{ln}\:{x}+\mathrm{1}\right)}{\mathrm{1}}={a}^{{a}} \left(\mathrm{ln}\:{a}+\mathrm{1}\right) \\ $$
