Question Number 158862 by mathlove last updated on 09/Nov/21
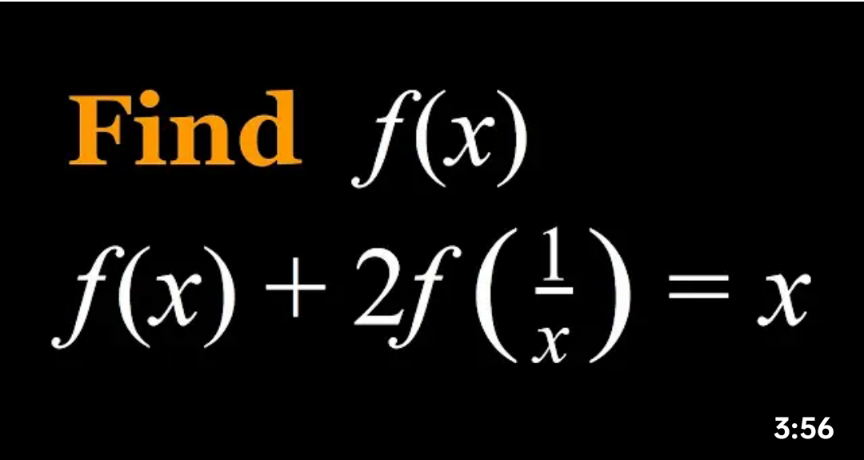
Answered by gsk2684 last updated on 09/Nov/21
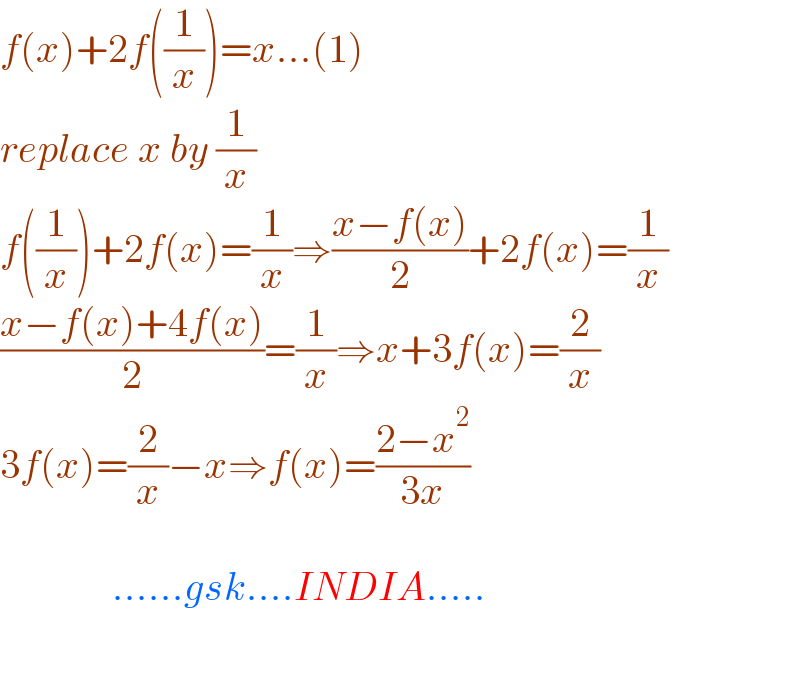
$${f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)={x}…\left(\mathrm{1}\right) \\ $$$${replace}\:{x}\:{by}\:\frac{\mathrm{1}}{{x}} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{2}{f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\Rightarrow\frac{{x}−{f}\left({x}\right)}{\mathrm{2}}+\mathrm{2}{f}\left({x}\right)=\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{x}−{f}\left({x}\right)+\mathrm{4}{f}\left({x}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{{x}}\Rightarrow{x}+\mathrm{3}{f}\left({x}\right)=\frac{\mathrm{2}}{{x}} \\ $$$$\mathrm{3}{f}\left({x}\right)=\frac{\mathrm{2}}{{x}}−{x}\Rightarrow{f}\left({x}\right)=\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{3}{x}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:……{gsk}….{INDIA}….. \\ $$$$ \\ $$
