Question Number 158874 by ajfour last updated on 09/Nov/21
Commented by ajfour last updated on 09/Nov/21

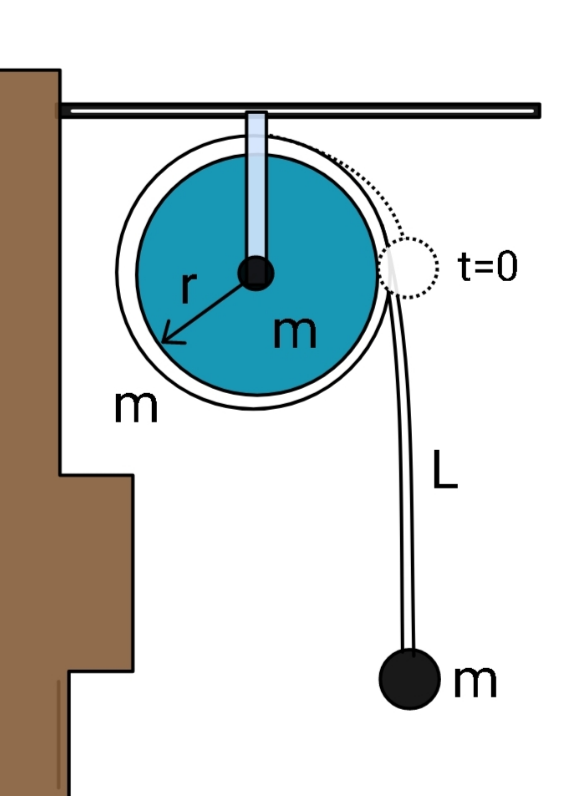
$${Length}\:{of}\:{rope}\:{is}\:{L},\:{mass}\:{m}. \\ $$$${The}\:{pulley}\:{even}\:{has}\:{mass}\:{m} \\ $$$${and}\:{radius}\:{is}\:{r}.\:{The}\:{bead}\:{has} \\ $$$${mass}\:{m}.\:{After}\:{release}\:{at}\:{t}=\mathrm{0}, \\ $$$${find}\:{v}\left({x}\right);\:{v}\:{being}\:{the}\:{speed}\:{of} \\ $$$${bead},\:{while}\:{x}\:{being}\:\:{hanging} \\ $$$${length}\:{of}\:{rope}. \\ $$
Answered by mr W last updated on 10/Nov/21
![at time t: I=((mr^2 )/2)+(1−(x/L))mr^2 =((mr^2 )/2)(3−((2x)/L)) M=m+(x/L)m=(1+(x/L))m ω=(v/r) v=(dx/dt) T=tension in hanging rope at pulley ((d(Iω))/dt)=Tr ((mr)/2)(3−((2x)/L))(dv/dt)−((mr)/2)×(2/L)v^2 =Tr ((3/2)−(x/L))(dv/dt)−(v^2 /L)=(T/m) ...(i) (d/dt)(Mv)=Mg−T M(dv/dt)+(m/L)v^2 =Mg−T (1+(x/L))(dv/dt)+(v^2 /L)=(1+(x/L))g−(T/m) ...(ii) (i)+(ii): ((3/2)−(x/L))(dv/dt)−(v^2 /L)+(1+(x/L))(dv/dt)+(v^2 /L)=(1+(x/L))g (dv/dt)=((2g)/5)(1+(x/L)) v(dv/dx)=((2g)/5)(1+(x/L)) vdv=((2g)/5)(1+(x/L))dx ∫_0 ^v vdv=((2g)/5)∫_0 ^x (1+(x/L))dx v^2 =((2g)/5)(2+(x/L))x ⇒v(x)=(√(((2gL)/5)(2+(x/L))((x/L)))) v_1 =v(L)=(√((6gL)/5)) ================== (dx/dt)=(√(((2gL)/5)(2+(x/L))((x/L)))) (d/dt)((x/L))=(√(((2g)/(5L))(2+(x/L))((x/L)))) (dξ/dt)=(√(((2g)/(5L))(2+ξ)ξ)) (√((5L)/(2g)))(dξ/( (√((2+ξ)ξ))))=dt (√((5L)/(2g)))∫_0 ^ξ (dξ/( (√((2+ξ)ξ))))=∫_0 ^t dt (√((5L)/(2g)))[2ln ((√(2+ξ))+(√ξ))]_0 ^ξ =t ⇒t(x)=(√((10L)/g))ln (((√(2+(x/L)))+(√(x/L)))/( (√2))) t_1 =t(L)=(√((10L)/g))ln (((√3)+1)/( (√2)))](https://www.tinkutara.com/question/Q158877.png)
$${at}\:{time}\:{t}: \\ $$$${I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}+\left(\mathrm{1}−\frac{{x}}{{L}}\right){mr}^{\mathrm{2}} =\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{3}−\frac{\mathrm{2}{x}}{{L}}\right) \\ $$$${M}={m}+\frac{{x}}{{L}}{m}=\left(\mathrm{1}+\frac{{x}}{{L}}\right){m} \\ $$$$\omega=\frac{{v}}{{r}} \\ $$$${v}=\frac{{dx}}{{dt}} \\ $$$${T}={tension}\:{in}\:{hanging}\:{rope}\:{at}\:{pulley} \\ $$$$ \\ $$$$\frac{{d}\left({I}\omega\right)}{{dt}}={Tr} \\ $$$$\frac{{mr}}{\mathrm{2}}\left(\mathrm{3}−\frac{\mathrm{2}{x}}{{L}}\right)\frac{{dv}}{{dt}}−\frac{{mr}}{\mathrm{2}}×\frac{\mathrm{2}}{{L}}{v}^{\mathrm{2}} ={Tr} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{{x}}{{L}}\right)\frac{{dv}}{{dt}}−\frac{{v}^{\mathrm{2}} }{{L}}=\frac{{T}}{{m}}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\frac{{d}}{{dt}}\left({Mv}\right)={Mg}−{T} \\ $$$${M}\frac{{dv}}{{dt}}+\frac{{m}}{{L}}{v}^{\mathrm{2}} ={Mg}−{T}\: \\ $$$$\left(\mathrm{1}+\frac{{x}}{{L}}\right)\frac{{dv}}{{dt}}+\frac{{v}^{\mathrm{2}} }{{L}}=\left(\mathrm{1}+\frac{{x}}{{L}}\right){g}−\frac{{T}}{{m}}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{{x}}{{L}}\right)\frac{{dv}}{{dt}}−\frac{{v}^{\mathrm{2}} }{{L}}+\left(\mathrm{1}+\frac{{x}}{{L}}\right)\frac{{dv}}{{dt}}+\frac{{v}^{\mathrm{2}} }{{L}}=\left(\mathrm{1}+\frac{{x}}{{L}}\right){g} \\ $$$$\frac{{dv}}{{dt}}=\frac{\mathrm{2}{g}}{\mathrm{5}}\left(\mathrm{1}+\frac{{x}}{{L}}\right) \\ $$$${v}\frac{{dv}}{{dx}}=\frac{\mathrm{2}{g}}{\mathrm{5}}\left(\mathrm{1}+\frac{{x}}{{L}}\right) \\ $$$${vdv}=\frac{\mathrm{2}{g}}{\mathrm{5}}\left(\mathrm{1}+\frac{{x}}{{L}}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{{v}} {vdv}=\frac{\mathrm{2}{g}}{\mathrm{5}}\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}+\frac{{x}}{{L}}\right){dx} \\ $$$${v}^{\mathrm{2}} =\frac{\mathrm{2}{g}}{\mathrm{5}}\left(\mathrm{2}+\frac{{x}}{{L}}\right){x} \\ $$$$\Rightarrow{v}\left({x}\right)=\sqrt{\frac{\mathrm{2}{gL}}{\mathrm{5}}\left(\mathrm{2}+\frac{{x}}{{L}}\right)\left(\frac{{x}}{{L}}\right)} \\ $$$${v}_{\mathrm{1}} ={v}\left({L}\right)=\sqrt{\frac{\mathrm{6}{gL}}{\mathrm{5}}} \\ $$$$================== \\ $$$$\frac{{dx}}{{dt}}=\sqrt{\frac{\mathrm{2}{gL}}{\mathrm{5}}\left(\mathrm{2}+\frac{{x}}{{L}}\right)\left(\frac{{x}}{{L}}\right)} \\ $$$$\frac{{d}}{{dt}}\left(\frac{{x}}{{L}}\right)=\sqrt{\frac{\mathrm{2}{g}}{\mathrm{5}{L}}\left(\mathrm{2}+\frac{{x}}{{L}}\right)\left(\frac{{x}}{{L}}\right)} \\ $$$$\frac{{d}\xi}{{dt}}=\sqrt{\frac{\mathrm{2}{g}}{\mathrm{5}{L}}\left(\mathrm{2}+\xi\right)\xi} \\ $$$$\sqrt{\frac{\mathrm{5}{L}}{\mathrm{2}{g}}}\frac{{d}\xi}{\:\sqrt{\left(\mathrm{2}+\xi\right)\xi}}={dt} \\ $$$$\sqrt{\frac{\mathrm{5}{L}}{\mathrm{2}{g}}}\int_{\mathrm{0}} ^{\xi} \frac{{d}\xi}{\:\sqrt{\left(\mathrm{2}+\xi\right)\xi}}=\int_{\mathrm{0}} ^{{t}} {dt} \\ $$$$\sqrt{\frac{\mathrm{5}{L}}{\mathrm{2}{g}}}\left[\mathrm{2ln}\:\left(\sqrt{\mathrm{2}+\xi}+\sqrt{\xi}\right)\right]_{\mathrm{0}} ^{\xi} ={t} \\ $$$$\Rightarrow{t}\left({x}\right)=\sqrt{\frac{\mathrm{10}{L}}{{g}}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}+\frac{{x}}{{L}}}+\sqrt{\frac{{x}}{{L}}}}{\:\sqrt{\mathrm{2}}} \\ $$$${t}_{\mathrm{1}} ={t}\left({L}\right)=\sqrt{\frac{\mathrm{10}{L}}{{g}}}\mathrm{ln}\:\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 09/Nov/21

$${Most}\:{beautiful}\:{solution}\:{i}'{ve} \\ $$$${followed},\:{coz}\:{u}'{ve}\:{presented} \\ $$$${it}\:{utterly}\:{nice}\:{way};\:{thank}\:{u}\:{sir}. \\ $$
Commented by mr W last updated on 10/Nov/21
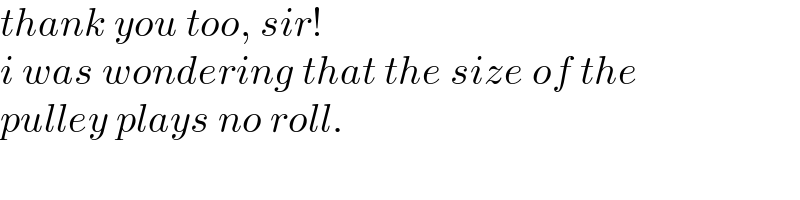
$${thank}\:{you}\:{too},\:{sir}! \\ $$$${i}\:{was}\:{wondering}\:{that}\:{the}\:{size}\:{of}\:{the} \\ $$$${pulley}\:{plays}\:{no}\:{roll}. \\ $$
Commented by ajfour last updated on 10/Nov/21

$${yes},\:{remarkable},\:{sir}.\:{And}\:{its}\: \\ $$$${really}\:{great}\:{that}\:{you}\:{even}\:{find} \\ $$$${the}\:{t}\left({x}\right);\:{which}\:{i}\:{had}\:{avoided}\: \\ $$$${asking}\:{thinking}\:{it}\:{just}\:{might} \\ $$$$\:{get}\:{too}\:{cumbersome}!\:{thanks}! \\ $$
Commented by Tawa11 last updated on 10/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 09/Nov/21
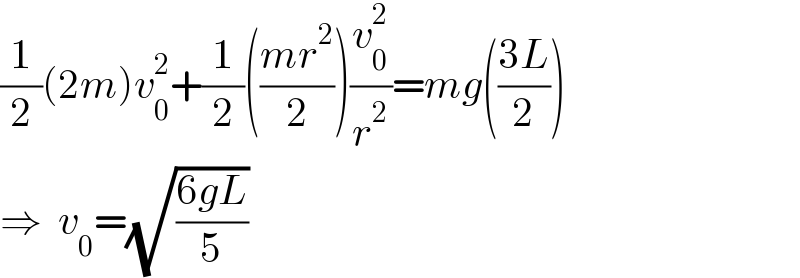
$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{m}\right){v}_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}\right)\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{{r}^{\mathrm{2}} }={mg}\left(\frac{\mathrm{3}{L}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\:{v}_{\mathrm{0}} =\sqrt{\frac{\mathrm{6}{gL}}{\mathrm{5}}} \\ $$
