Question Number 158884 by akolade last updated on 10/Nov/21
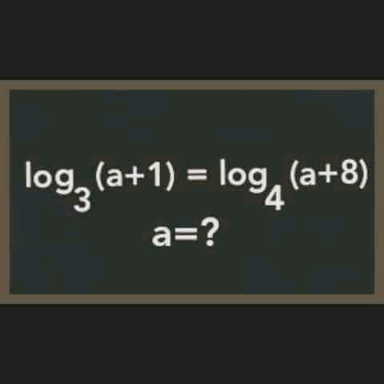
Answered by ghimisi last updated on 10/Nov/21
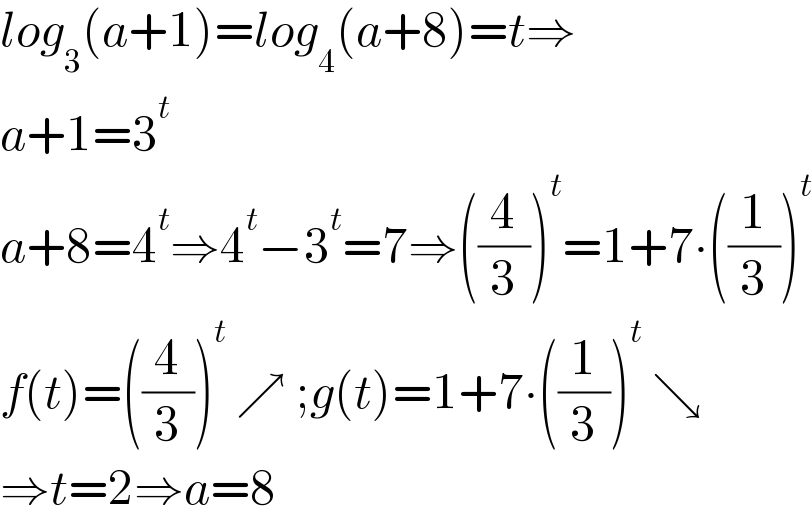
$${log}_{\mathrm{3}} \left({a}+\mathrm{1}\right)={log}_{\mathrm{4}} \left({a}+\mathrm{8}\right)={t}\Rightarrow \\ $$$${a}+\mathrm{1}=\mathrm{3}^{{t}} \\ $$$${a}+\mathrm{8}=\mathrm{4}^{{t}} \Rightarrow\mathrm{4}^{{t}} −\mathrm{3}^{{t}} =\mathrm{7}\Rightarrow\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{t}} =\mathrm{1}+\mathrm{7}\centerdot\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{t}} \\ $$$${f}\left({t}\right)=\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{t}} \:\nearrow\:;{g}\left({t}\right)=\mathrm{1}+\mathrm{7}\centerdot\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{t}} \:\searrow \\ $$$$\Rightarrow{t}=\mathrm{2}\Rightarrow{a}=\mathrm{8} \\ $$
