Question Number 158894 by mathlove last updated on 10/Nov/21
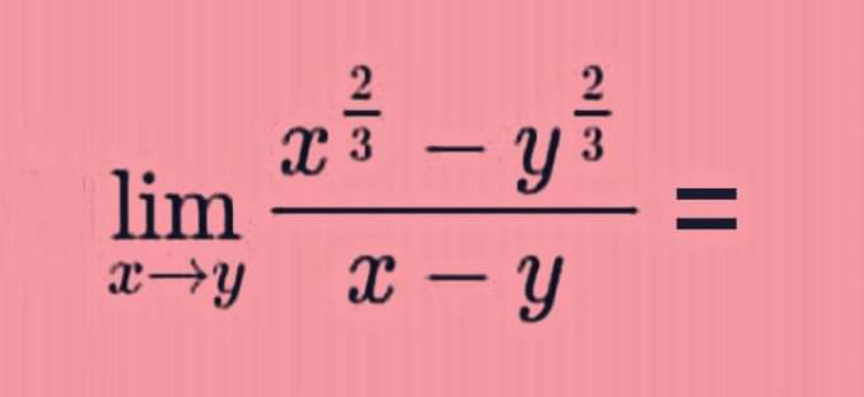
Commented by cortano last updated on 10/Nov/21
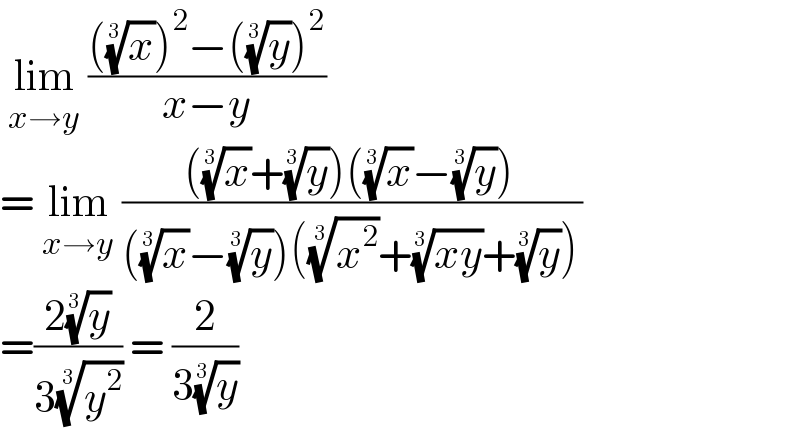
$$\:\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\left(\sqrt[{\mathrm{3}}]{{x}}\right)^{\mathrm{2}} −\left(\sqrt[{\mathrm{3}}]{{y}}\right)^{\mathrm{2}} }{{x}−{y}} \\ $$$$=\:\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\left(\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{3}}]{{y}}\right)\left(\sqrt[{\mathrm{3}}]{{x}}−\sqrt[{\mathrm{3}}]{{y}}\right)}{\left(\sqrt[{\mathrm{3}}]{{x}}−\sqrt[{\mathrm{3}}]{{y}}\right)\left(\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{{xy}}+\sqrt[{\mathrm{3}}]{{y}}\right)} \\ $$$$=\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{{y}}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{y}^{\mathrm{2}} }}\:=\:\frac{\mathrm{2}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{y}}}\: \\ $$
