Question Number 158927 by cherokeesay last updated on 10/Nov/21

Answered by amin96 last updated on 10/Nov/21
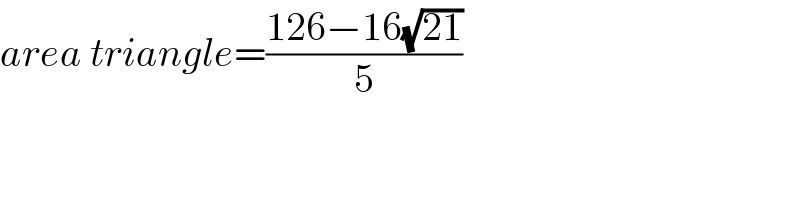
$${area}\:{triangle}=\frac{\mathrm{126}−\mathrm{16}\sqrt{\mathrm{21}}}{\mathrm{5}} \\ $$
Commented by cherokeesay last updated on 10/Nov/21

$${thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 10/Nov/21
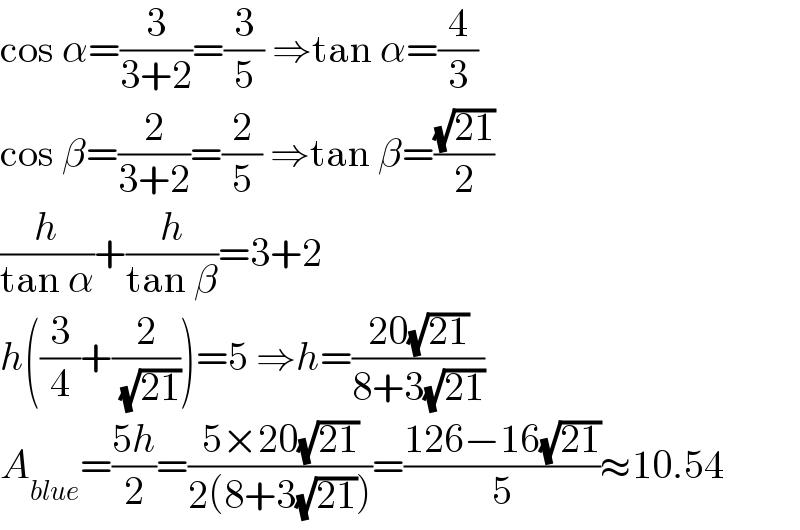
$$\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\mathrm{3}+\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{5}}\:\Rightarrow\mathrm{tan}\:\beta=\frac{\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\frac{{h}}{\mathrm{tan}\:\alpha}+\frac{{h}}{\mathrm{tan}\:\beta}=\mathrm{3}+\mathrm{2} \\ $$$${h}\left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{21}}}\right)=\mathrm{5}\:\Rightarrow{h}=\frac{\mathrm{20}\sqrt{\mathrm{21}}}{\mathrm{8}+\mathrm{3}\sqrt{\mathrm{21}}} \\ $$$${A}_{{blue}} =\frac{\mathrm{5}{h}}{\mathrm{2}}=\frac{\mathrm{5}×\mathrm{20}\sqrt{\mathrm{21}}}{\mathrm{2}\left(\mathrm{8}+\mathrm{3}\sqrt{\mathrm{21}}\right)}=\frac{\mathrm{126}−\mathrm{16}\sqrt{\mathrm{21}}}{\mathrm{5}}\approx\mathrm{10}.\mathrm{54} \\ $$
Commented by cherokeesay last updated on 10/Nov/21

$${very}\:{nice}\:! \\ $$$${thank}\:{you}\:{sir}\:! \\ $$
Commented by Tawa11 last updated on 11/Nov/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
