Question Number 158955 by mr W last updated on 11/Nov/21

Answered by mr W last updated on 15/Nov/21
![let′s look at the general case with n students into r schools. both students (objects) and schools (boxes) are distinct. let′s say the school S_1 obtains n_1 students, the schools S_2 obtains n_2 students, etc. n_1 +n_2 +n_3 +...+n_r =n 1) no restriction: n_1 ≥0, n_2 ≥0, etc. 2) each schools obtains at least one student: n_1 ≥1, n_2 ≥1, etc. to distribute n students into r schools such that S_1 obtains n_1 students, S_2 obtains n_2 students, etc. and S_r obtains n_r students, there are C_n_1 ^n C_n_2 ^(n−n_1 ) ...C_n_r ^(n−n_1 −n_2 −...−n_(r−1) ) ways, which is ((n!)/(n!(n−n_1 )!))×(((n−n_1 )!)/(n_2 !(n−n_1 −n_2 )!))×...×(((n−n_1 −n_2 −...−n_(r−1) )!)/(n_r !0!)), i.e. ((n!)/(n_1 !n_2 !n_3 !...n_r !)) ways. using generating function method we can see that for case 1) number of ways is the coef. of x^n in n!(1+(x/(1!))+(x^2 /(2!))+(x^3 /(3!))+...)^r =n!(e^x )^r =n!e^(rx) =n!(1+((rx)/(1!))+((r^2 x^2 )/(2!))+((r^3 x^3 )/(3!))+...) coef. of x^n is n!×(r^n /(n!))=r^n . that means there are r^n ways to distribute n students into r schools without restriction. for case 2) number of ways is the coef. of x^n in n!((x/(1!))+(x^2 /(2!))+(x^3 /(3!))+...)^r =n!(e^x −1)^r =n!Σ_(k=0) ^r (−1)^k C_k ^r (e^x )^(r−k) =n!Σ_(k=0) ^r {(−1)^k C_k ^r [1+(((r−k)x)/(1!))+(((r−k)^2 x^2 )/(2!))+...]} the coef. of x^n is n!Σ_(k=0) ^r [(−1)^k C_k ^r (((r−k)^n )/(n!))] =Σ_(k=0) ^r (−1)^k C_k ^r (r−k)^n = r^n −C_1 ^r (r−1)^n +C_2 ^r (r−2)^n −...+(−1)^(r−1) C_(r−1) ^r](https://www.tinkutara.com/question/Q158956.png)
$${let}'{s}\:{look}\:{at}\:{the}\:{general}\:{case}\:{with}\:{n} \\ $$$${students}\:{into}\:{r}\:{schools}.\:{both}\:{students} \\ $$$$\left({objects}\right)\:{and}\:{schools}\:\left({boxes}\right)\:{are} \\ $$$${distinct}. \\ $$$${let}'{s}\:{say}\:{the}\:{school}\:{S}_{\mathrm{1}} \:{obtains}\:{n}_{\mathrm{1}} \: \\ $$$${students},\:{the}\:{schools}\:{S}_{\mathrm{2}} \:{obtains}\:{n}_{\mathrm{2}} \\ $$$${students},\:{etc}. \\ $$$${n}_{\mathrm{1}} +{n}_{\mathrm{2}} +{n}_{\mathrm{3}} +…+{n}_{{r}} ={n} \\ $$$$\left.\mathrm{1}\right)\:{no}\:{restriction}:\:{n}_{\mathrm{1}} \geqslant\mathrm{0},\:{n}_{\mathrm{2}} \geqslant\mathrm{0},\:{etc}. \\ $$$$\left.\mathrm{2}\right)\:{each}\:{schools}\:{obtains}\:{at}\:{least}\:{one} \\ $$$${student}:\:{n}_{\mathrm{1}} \geqslant\mathrm{1},\:{n}_{\mathrm{2}} \geqslant\mathrm{1},\:{etc}. \\ $$$$ \\ $$$${to}\:{distribute}\:{n}\:{students}\:{into}\:{r}\:{schools} \\ $$$${such}\:{that}\:{S}_{\mathrm{1}} \:{obtains}\:{n}_{\mathrm{1}} \:{students}, \\ $$$${S}_{\mathrm{2}} \:{obtains}\:{n}_{\mathrm{2}} \:{students},\:{etc}.\:{and} \\ $$$${S}_{{r}} \:{obtains}\:{n}_{{r}} \:{students},\:{there}\:{are} \\ $$$${C}_{{n}_{\mathrm{1}} } ^{{n}} {C}_{{n}_{\mathrm{2}} } ^{{n}−{n}_{\mathrm{1}} } …{C}_{{n}_{{r}} } ^{{n}−{n}_{\mathrm{1}} −{n}_{\mathrm{2}} −…−{n}_{{r}−\mathrm{1}} } \:{ways}, \\ $$$${which}\:{is} \\ $$$$\frac{{n}!}{{n}!\left({n}−{n}_{\mathrm{1}} \right)!}×\frac{\left({n}−{n}_{\mathrm{1}} \right)!}{{n}_{\mathrm{2}} !\left({n}−{n}_{\mathrm{1}} −{n}_{\mathrm{2}} \right)!}×…×\frac{\left({n}−{n}_{\mathrm{1}} −{n}_{\mathrm{2}} −…−{n}_{{r}−\mathrm{1}} \right)!}{{n}_{{r}} !\mathrm{0}!}, \\ $$$${i}.{e}.\:\frac{{n}!}{{n}_{\mathrm{1}} !{n}_{\mathrm{2}} !{n}_{\mathrm{3}} !…{n}_{{r}} !}\:{ways}. \\ $$$${using}\:{generating}\:{function}\:{method} \\ $$$${we}\:{can}\:{see}\:{that} \\ $$$$\left.\underline{\boldsymbol{{for}}\:\boldsymbol{{case}}\:\mathrm{1}\right)} \\ $$$${number}\:{of}\:{ways}\:{is}\:{the}\:{coef}.\:{of}\:{x}^{{n}} \:{in} \\ $$$${n}!\left(\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…\right)^{{r}} \\ $$$$={n}!\left({e}^{{x}} \right)^{{r}} \\ $$$$={n}!{e}^{{rx}} \\ $$$$={n}!\left(\mathrm{1}+\frac{{rx}}{\mathrm{1}!}+\frac{{r}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{r}^{\mathrm{3}} {x}^{\mathrm{3}} }{\mathrm{3}!}+…\right) \\ $$$${coef}.\:{of}\:{x}^{{n}} \:{is}\:{n}!×\frac{{r}^{{n}} }{{n}!}={r}^{{n}} . \\ $$$${that}\:{means}\:{there}\:{are}\:{r}^{{n}} \:{ways}\:{to} \\ $$$${distribute}\:{n}\:{students}\:{into}\:{r}\:{schools} \\ $$$${without}\:{restriction}. \\ $$$$\left.\underline{\boldsymbol{{for}}\:\boldsymbol{{case}}\:\mathrm{2}\right)} \\ $$$${number}\:{of}\:{ways}\:{is}\:{the}\:{coef}.\:{of}\:{x}^{{n}} \:{in} \\ $$$${n}!\left(\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…\right)^{{r}} \\ $$$$={n}!\left({e}^{{x}} −\mathrm{1}\right)^{{r}} \\ $$$$={n}!\underset{{k}=\mathrm{0}} {\overset{{r}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{r}} \left({e}^{{x}} \right)^{{r}−{k}} \\ $$$$={n}!\underset{{k}=\mathrm{0}} {\overset{{r}} {\sum}}\left\{\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{r}} \left[\mathrm{1}+\frac{\left({r}−{k}\right){x}}{\mathrm{1}!}+\frac{\left({r}−{k}\right)^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}!}+…\right]\right\} \\ $$$${the}\:{coef}.\:{of}\:{x}^{{n}} \:{is} \\ $$$${n}!\underset{{k}=\mathrm{0}} {\overset{{r}} {\sum}}\left[\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{r}} \frac{\left({r}−{k}\right)^{{n}} }{{n}!}\right] \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{r}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{r}} \left({r}−{k}\right)^{{n}} \\ $$$$=\:{r}^{{n}} −{C}_{\mathrm{1}} ^{{r}} \left({r}−\mathrm{1}\right)^{{n}} +{C}_{\mathrm{2}} ^{{r}} \left({r}−\mathrm{2}\right)^{{n}} −…+\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {C}_{{r}−\mathrm{1}} ^{{r}} \\ $$
Commented by Tawa11 last updated on 11/Nov/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 11/Nov/21
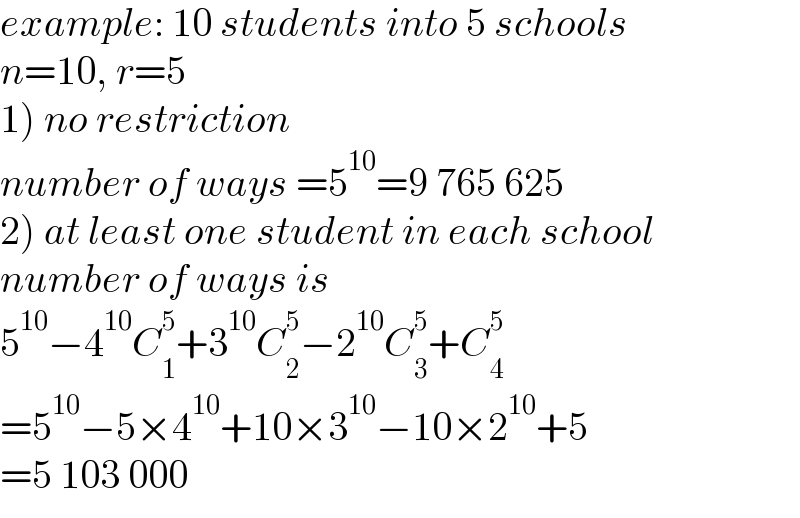
$${example}:\:\mathrm{10}\:{students}\:{into}\:\mathrm{5}\:{schools} \\ $$$${n}=\mathrm{10},\:{r}=\mathrm{5} \\ $$$$\left.\mathrm{1}\right)\:{no}\:{restriction} \\ $$$${number}\:{of}\:{ways}\:=\mathrm{5}^{\mathrm{10}} =\mathrm{9}\:\mathrm{765}\:\mathrm{625} \\ $$$$\left.\mathrm{2}\right)\:{at}\:{least}\:{one}\:{student}\:{in}\:{each}\:{school} \\ $$$${number}\:{of}\:{ways}\:{is} \\ $$$$\mathrm{5}^{\mathrm{10}} −\mathrm{4}^{\mathrm{10}} {C}_{\mathrm{1}} ^{\mathrm{5}} +\mathrm{3}^{\mathrm{10}} {C}_{\mathrm{2}} ^{\mathrm{5}} −\mathrm{2}^{\mathrm{10}} {C}_{\mathrm{3}} ^{\mathrm{5}} +{C}_{\mathrm{4}} ^{\mathrm{5}} \\ $$$$=\mathrm{5}^{\mathrm{10}} −\mathrm{5}×\mathrm{4}^{\mathrm{10}} +\mathrm{10}×\mathrm{3}^{\mathrm{10}} −\mathrm{10}×\mathrm{2}^{\mathrm{10}} +\mathrm{5} \\ $$$$=\mathrm{5}\:\mathrm{103}\:\mathrm{000} \\ $$
Commented by otchereabdullai@gmail.com last updated on 12/Nov/21

$$\mathrm{more}\:\mathrm{blessing}\:\mathrm{prof}! \\ $$
