Question Number 158961 by ajfour last updated on 11/Nov/21
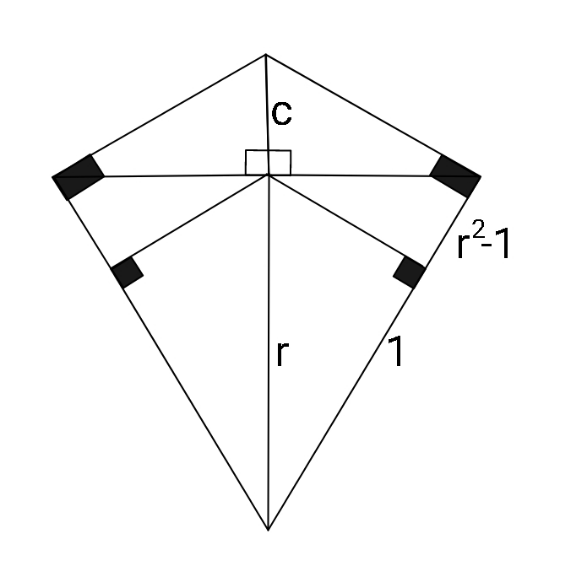
Commented by ajfour last updated on 11/Nov/21
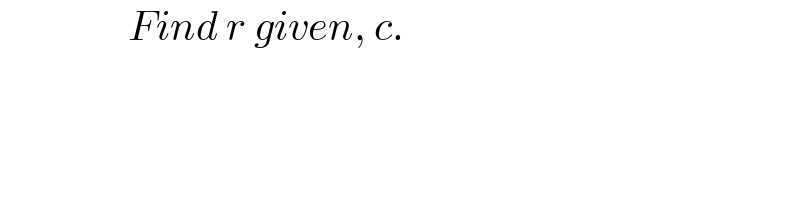
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Find}\:{r}\:{given},\:{c}. \\ $$
Commented by 1549442205PVT last updated on 11/Nov/21
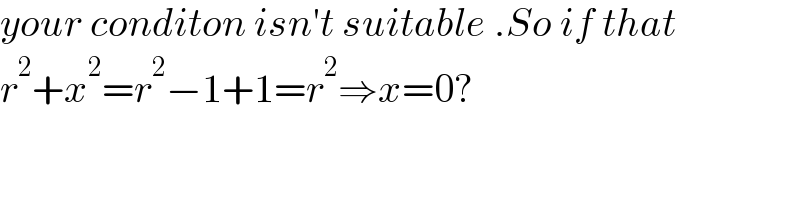
$${your}\:{conditon}\:{isn}'{t}\:{suitable}\:.{So}\:{if}\:{that} \\ $$$${r}^{\mathrm{2}} +{x}^{\mathrm{2}} ={r}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}={r}^{\mathrm{2}} \Rightarrow{x}=\mathrm{0}? \\ $$
Commented by 1549442205PVT last updated on 13/Nov/21

$${Ecxcuse}\:{me},{i}\:{mistake}!{Thank}\:{you}\:{sir} \\ $$$${for}\:{interesting}\:{problems}. \\ $$
Answered by ajfour last updated on 12/Nov/21
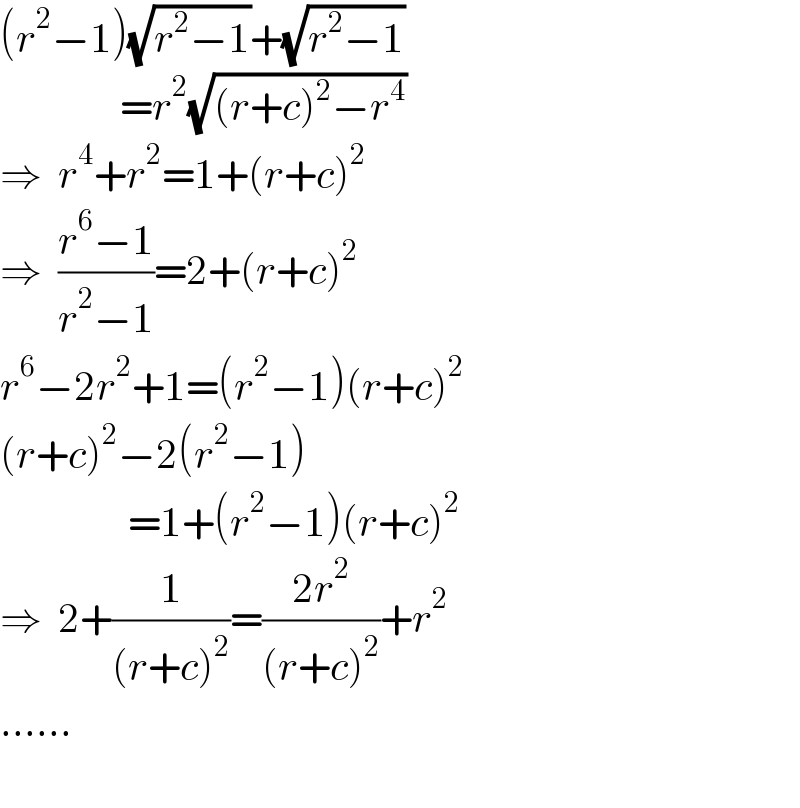
$$\left({r}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{r}^{\mathrm{2}} −\mathrm{1}}+\sqrt{{r}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={r}^{\mathrm{2}} \sqrt{\left({r}+{c}\right)^{\mathrm{2}} −{r}^{\mathrm{4}} } \\ $$$$\Rightarrow\:\:{r}^{\mathrm{4}} +{r}^{\mathrm{2}} =\mathrm{1}+\left({r}+{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{{r}^{\mathrm{6}} −\mathrm{1}}{{r}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2}+\left({r}+{c}\right)^{\mathrm{2}} \\ $$$${r}^{\mathrm{6}} −\mathrm{2}{r}^{\mathrm{2}} +\mathrm{1}=\left({r}^{\mathrm{2}} −\mathrm{1}\right)\left({r}+{c}\right)^{\mathrm{2}} \\ $$$$\left({r}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({r}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\left({r}^{\mathrm{2}} −\mathrm{1}\right)\left({r}+{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}+\frac{\mathrm{1}}{\left({r}+{c}\right)^{\mathrm{2}} }=\frac{\mathrm{2}{r}^{\mathrm{2}} }{\left({r}+{c}\right)^{\mathrm{2}} }+{r}^{\mathrm{2}} \\ $$$$…… \\ $$$$ \\ $$
