Menu Close

Question-158988

Tinku Tara 0 Comments
Pin




Question Number 158988 by cortano last updated on 11/Nov/21
Answered by Rasheed.Sindhi last updated on 11/Nov/21
The graph of f(x) intersects y=2x−1 at x=1,2,3 ∴ The points of intersections: (1,2(1)−1) , (2,2(2)−1) &(3,2(3)−1) Or (1,1),(2,3) & (3,5) also the points on f(x): (1,1): f(1)=(1)^4 +a(1)^3 +b(1)^2 +c(1)+d=1 ⇒a+b+c+d=0............A (2,3): f(2)=(2)^4 +a(2)^3 +b(2)^2 +c(2)+d=3 ⇒8a+4b+2c+d=−13.....B (3,5): f(3)=(3)^4 +a(3)^3 +b(3)^2 +c(3)+d=5 ⇒27a+9b+3c+d=−76........C f(0)=d f(4)=4^4 +a(4)^3 +b(4)^2 +c(4)+d=e(say) =256+64a+16b+4c+d f(0)+f(4)=256+64a+16b+4c+2d =256+64a+16b+4c+2d =256+64a+16b+2(−13−8a−4b) =230+48a+8b f(0)+f(4)=230+8(6a+b) B−A:7a+3b+c=−13...........D C−B: 19a+5b+c=−63........E E−D:12a+2b=−50⇒6a+b=−25 f(0)+f(4)=230+8(6a+b) =230+8(−25)=30
$$\mathcal{T}{he}\:{graph}\:{of}\:{f}\left({x}\right)\:{intersects}\:{y}=\mathrm{2}{x}−\mathrm{1} \\ $$$${at}\:{x}=\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\therefore\:\mathcal{T}{he}\:{points}\:{of}\:{intersections}: \\ $$$$\:\:\:\:\:\:\left(\mathrm{1},\mathrm{2}\left(\mathrm{1}\right)−\mathrm{1}\right)\:,\:\left(\mathrm{2},\mathrm{2}\left(\mathrm{2}\right)−\mathrm{1}\right)\:\&\left(\mathrm{3},\mathrm{2}\left(\mathrm{3}\right)−\mathrm{1}\right) \\ $$$$\:\:\:{Or}\:\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{3}\right)\:\&\:\left(\mathrm{3},\mathrm{5}\right)\: \\ $$$$\:\:\:\:{also}\:{the}\:{points}\:{on}\:{f}\left({x}\right): \\ $$$$\left(\mathrm{1},\mathrm{1}\right): \\ $$$${f}\left(\mathrm{1}\right)=\left(\mathrm{1}\right)^{\mathrm{4}} +{a}\left(\mathrm{1}\right)^{\mathrm{3}} +{b}\left(\mathrm{1}\right)^{\mathrm{2}} +{c}\left(\mathrm{1}\right)+{d}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow{a}+{b}+{c}+{d}=\mathrm{0}…………{A} \\ $$$$\left(\mathrm{2},\mathrm{3}\right): \\ $$$${f}\left(\mathrm{2}\right)=\left(\mathrm{2}\right)^{\mathrm{4}} +{a}\left(\mathrm{2}\right)^{\mathrm{3}} +{b}\left(\mathrm{2}\right)^{\mathrm{2}} +{c}\left(\mathrm{2}\right)+{d}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+{d}=−\mathrm{13}…..{B} \\ $$$$\left(\mathrm{3},\mathrm{5}\right): \\ $$$${f}\left(\mathrm{3}\right)=\left(\mathrm{3}\right)^{\mathrm{4}} +{a}\left(\mathrm{3}\right)^{\mathrm{3}} +{b}\left(\mathrm{3}\right)^{\mathrm{2}} +{c}\left(\mathrm{3}\right)+{d}=\mathrm{5} \\ $$$$\:\:\:\:\Rightarrow\mathrm{27}{a}+\mathrm{9}{b}+\mathrm{3}{c}+{d}=−\mathrm{76}……..{C} \\ $$$${f}\left(\mathrm{0}\right)={d} \\ $$$${f}\left(\mathrm{4}\right)=\mathrm{4}^{\mathrm{4}} +{a}\left(\mathrm{4}\right)^{\mathrm{3}} +{b}\left(\mathrm{4}\right)^{\mathrm{2}} +{c}\left(\mathrm{4}\right)+{d}={e}\left({say}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{256}+\mathrm{64}{a}+\mathrm{16}{b}+\mathrm{4}{c}+{d} \\ $$$${f}\left(\mathrm{0}\right)+{f}\left(\mathrm{4}\right)=\mathrm{256}+\mathrm{64}{a}+\mathrm{16}{b}+\mathrm{4}{c}+\mathrm{2}{d} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{256}+\mathrm{64}{a}+\mathrm{16}{b}+\mathrm{4}{c}+\mathrm{2}{d} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{256}+\mathrm{64}{a}+\mathrm{16}{b}+\mathrm{2}\left(−\mathrm{13}−\mathrm{8}{a}−\mathrm{4}{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{230}+\mathrm{48}{a}+\mathrm{8}{b} \\ $$$$\:{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{4}\right)=\mathrm{230}+\mathrm{8}\left(\mathrm{6}{a}+{b}\right) \\ $$$${B}−{A}:\mathrm{7}{a}+\mathrm{3}{b}+{c}=−\mathrm{13}………..{D} \\ $$$${C}−{B}:\:\mathrm{19}{a}+\mathrm{5}{b}+{c}=−\mathrm{63}……..{E} \\ $$$${E}−{D}:\mathrm{12}{a}+\mathrm{2}{b}=−\mathrm{50}\Rightarrow\mathrm{6}{a}+{b}=−\mathrm{25} \\ $$$$\:{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{4}\right)=\mathrm{230}+\mathrm{8}\left(\mathrm{6}{a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{230}+\mathrm{8}\left(−\mathrm{25}\right)=\mathrm{30} \\ $$
Commented by cortano last updated on 13/Nov/21
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mr W last updated on 11/Nov/21
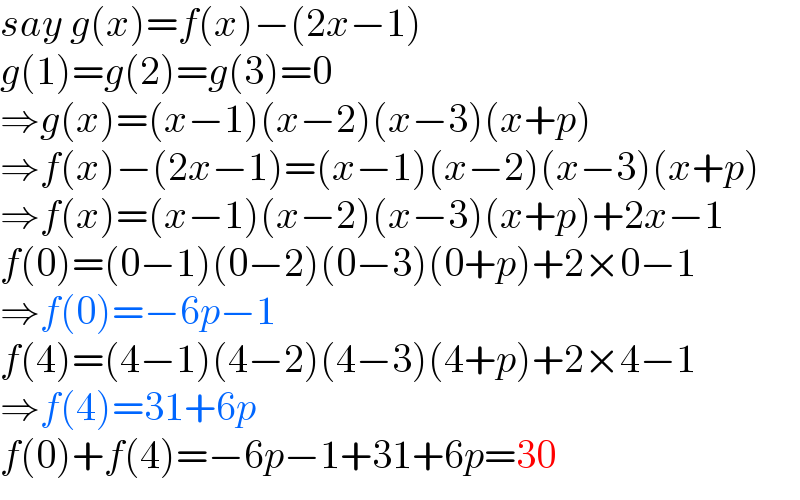
say g(x)=f(x)−(2x−1) g(1)=g(2)=g(3)=0 ⇒g(x)=(x−1)(x−2)(x−3)(x+p) ⇒f(x)−(2x−1)=(x−1)(x−2)(x−3)(x+p) ⇒f(x)=(x−1)(x−2)(x−3)(x+p)+2x−1 f(0)=(0−1)(0−2)(0−3)(0+p)+2×0−1 ⇒f(0)=−6p−1 f(4)=(4−1)(4−2)(4−3)(4+p)+2×4−1 ⇒f(4)=31+6p f(0)+f(4)=−6p−1+31+6p=30
$${say}\:{g}\left({x}\right)={f}\left({x}\right)−\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$${g}\left(\mathrm{1}\right)={g}\left(\mathrm{2}\right)={g}\left(\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{g}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}+{p}\right) \\ $$$$\Rightarrow{f}\left({x}\right)−\left(\mathrm{2}{x}−\mathrm{1}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}+{p}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}+{p}\right)+\mathrm{2}{x}−\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\left(\mathrm{0}−\mathrm{1}\right)\left(\mathrm{0}−\mathrm{2}\right)\left(\mathrm{0}−\mathrm{3}\right)\left(\mathrm{0}+{p}\right)+\mathrm{2}×\mathrm{0}−\mathrm{1} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)=−\mathrm{6}{p}−\mathrm{1} \\ $$$${f}\left(\mathrm{4}\right)=\left(\mathrm{4}−\mathrm{1}\right)\left(\mathrm{4}−\mathrm{2}\right)\left(\mathrm{4}−\mathrm{3}\right)\left(\mathrm{4}+{p}\right)+\mathrm{2}×\mathrm{4}−\mathrm{1} \\ $$$$\Rightarrow{f}\left(\mathrm{4}\right)=\mathrm{31}+\mathrm{6}{p} \\ $$$${f}\left(\mathrm{0}\right)+{f}\left(\mathrm{4}\right)=−\mathrm{6}{p}−\mathrm{1}+\mathrm{31}+\mathrm{6}{p}=\mathrm{30} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Nov/21
A Novel Method! Wonderful Sir!
$${A}\:{Novel}\:{Method}! \\ $$$${Wonderful}\:\mathcal{S}{ir}! \\ $$
Commented by mr W last updated on 12/Nov/21
thanks sir! we see again: many roads lead to Rome!
$${thanks}\:{sir}!\:{we}\:{see}\:{again}: \\ $$$${many}\:{roads}\:{lead}\:{to}\:{Rome}! \\ $$
Commented by Rasheed.Sindhi last updated on 12/Nov/21
Of course sir! I′m always interested in ′many roads′ that is variety of solutions. But after all some roads are better than others!
$${Of}\:{course}\:{sir}! \\ $$$${I}'{m}\:{always}\:{interested}\:{in}\:'{many} \\ $$$${roads}'\:\:{that}\:{is}\:{variety}\:{of}\:{solutions}. \\ $$$${But}\:{after}\:{all}\:{some}\:{roads}\:{are}\:{better} \\ $$$${than}\:{others}! \\ $$
Commented by cortano last updated on 13/Nov/21
nice
$${nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *