Question Number 159021 by Abdissalammjr last updated on 11/Nov/21
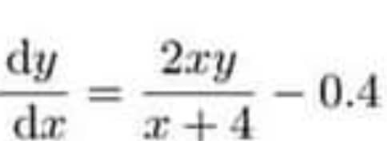
Answered by mkam last updated on 11/Nov/21
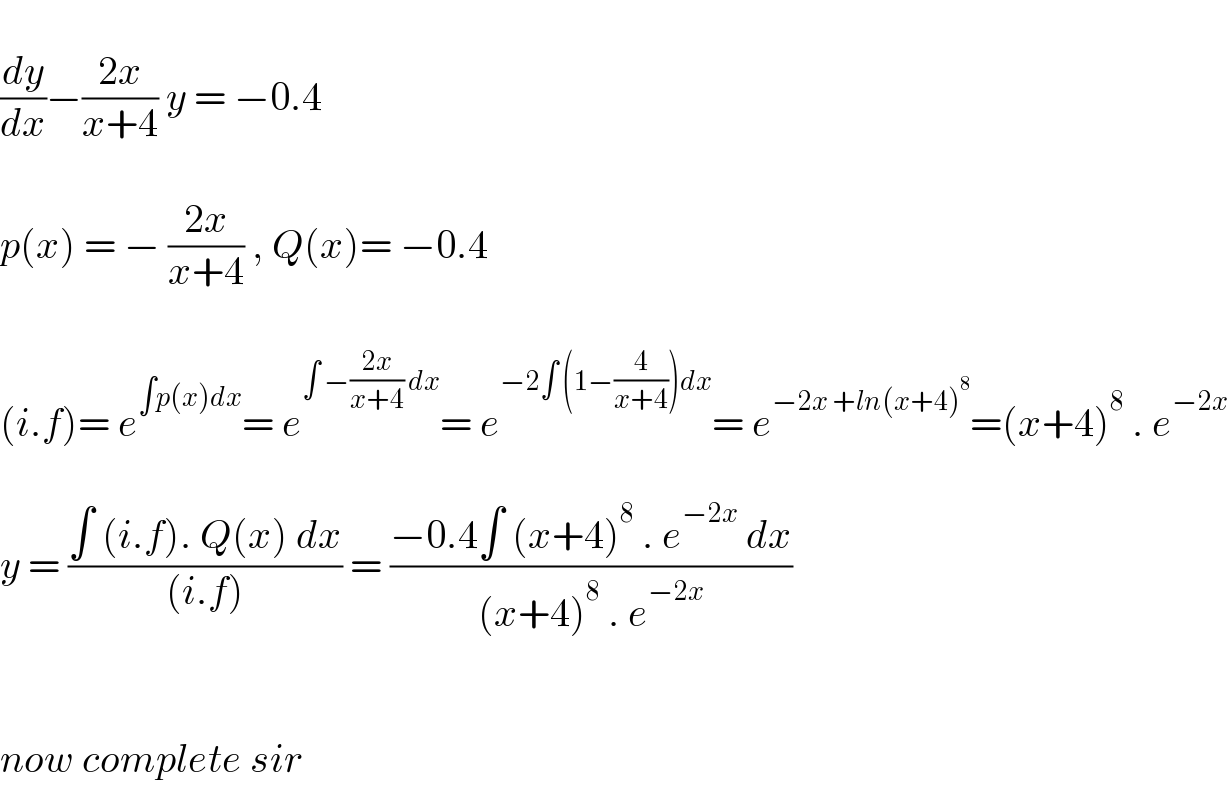
$$ \\ $$$$\frac{{dy}}{{dx}}−\frac{\mathrm{2}{x}}{{x}+\mathrm{4}}\:{y}\:=\:−\mathrm{0}.\mathrm{4} \\ $$$$ \\ $$$${p}\left({x}\right)\:=\:−\:\frac{\mathrm{2}{x}}{{x}+\mathrm{4}}\:,\:{Q}\left({x}\right)=\:−\mathrm{0}.\mathrm{4} \\ $$$$ \\ $$$$\left({i}.{f}\right)=\:{e}^{\int{p}\left({x}\right){dx}} =\:{e}^{\int\:−\frac{\mathrm{2}{x}}{{x}+\mathrm{4}}\:{dx}} =\:{e}^{−\mathrm{2}\int\:\left(\mathrm{1}−\frac{\mathrm{4}}{{x}+\mathrm{4}}\right){dx}} =\:{e}^{−\mathrm{2}{x}\:+{ln}\left({x}+\mathrm{4}\right)^{\mathrm{8}} } =\left({x}+\mathrm{4}\right)^{\mathrm{8}} \:.\:{e}^{−\mathrm{2}{x}} \\ $$$$ \\ $$$${y}\:=\:\frac{\int\:\left({i}.{f}\right).\:{Q}\left({x}\right)\:{dx}}{\left({i}.{f}\right)}\:=\:\frac{−\mathrm{0}.\mathrm{4}\int\:\left({x}+\mathrm{4}\right)^{\mathrm{8}} \:.\:{e}^{−\mathrm{2}{x}} \:{dx}}{\left({x}+\mathrm{4}\right)^{\mathrm{8}} \:.\:{e}^{−\mathrm{2}{x}} } \\ $$$$ \\ $$$$ \\ $$$${now}\:{complete}\:{sir} \\ $$
