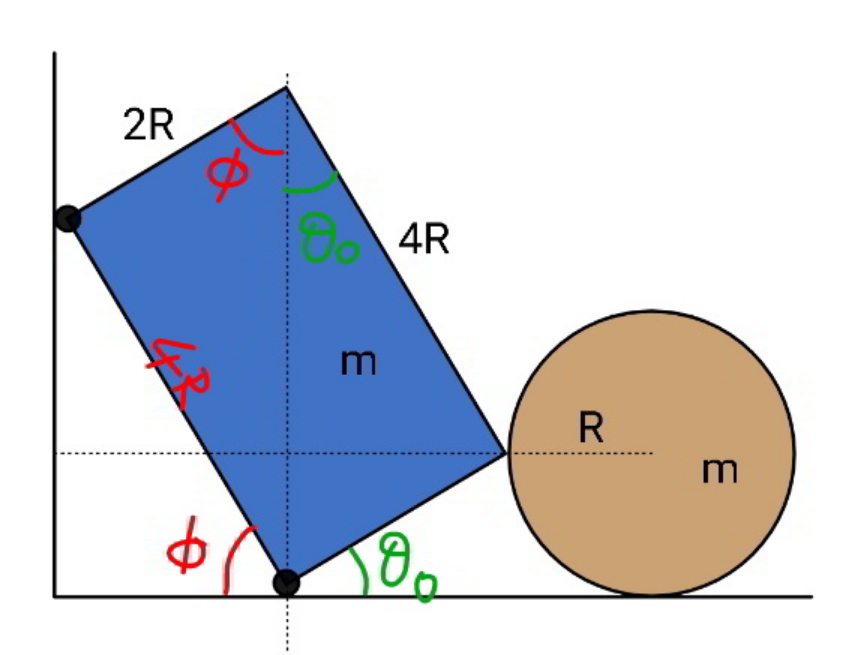
Question Number 159085 by ajfour last updated on 12/Nov/21
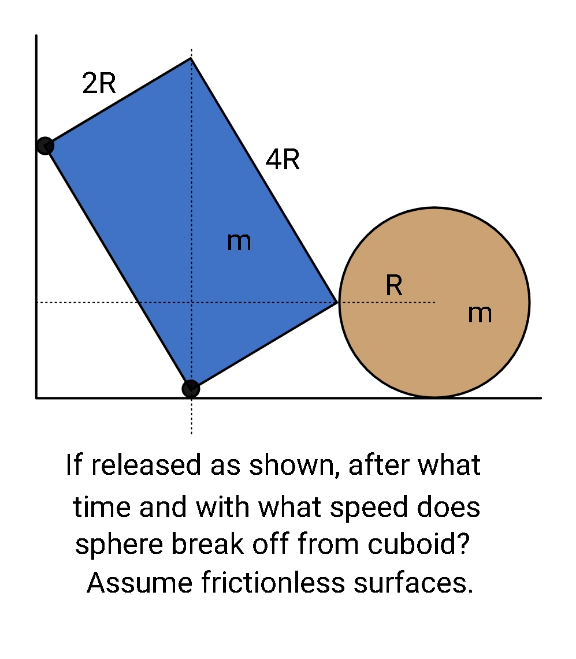
Answered by mr W last updated on 15/Nov/21
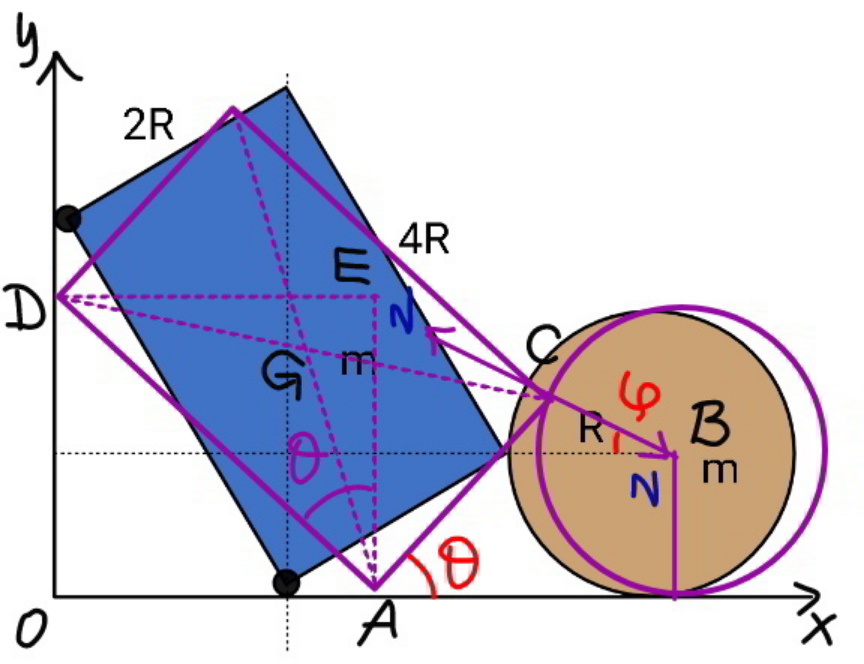
Commented by mr W last updated on 15/Nov/21
![2Rsin θ=R+Rsin ϕ sin ϕ=2 sin θ−1 (dϕ/dθ)=((2 cos θ)/(cos ϕ))=((cos θ)/( (√(sin θ(1−sin θ))))) x_A =x_E =4R sin θ x_B =x_A +2R cos θ+R cos ϕ x_B =4R sin θ+2R cos θ+R cos ϕ ω=(dθ/dt) v_B =(dx_B /dt)=4Rcos θ ω−2R sin θ ω−R sin ϕ ω (dϕ/dθ) v_B =2R(2cos θ−sin θ−cos θ tan ϕ)ω (dv_B /dθ)=2R(2cos θ−sin θ−cos θ tan ϕ)(dω/dθ) +2Rω(−2sin θ−cos θ+sin θ tan ϕ−((2cos^2 θ)/(cos^3 ϕ))) a_B =(dv_B /dt)=ω(dv_B /dθ) =2Rω(2cos θ−sin θ−cos θ tan ϕ)(dω/dθ) +2Rω^2 (−2sin θ−cos θ+sin θ tan ϕ−((2cos^2 θ)/(cos^3 ϕ))) Ncos ϕ=ma_B N=0 ⇒a_B =0 (2cos θ−sin θ−cos θ tan ϕ)(dω/dθ) −ω(2sin θ+cos θ−sin θ tan ϕ+((2cos^2 θ)/(cos^3 ϕ)))=0 ..(I) x_G −x_A =(−2sin θ+cos θ)R y_G =2R cos θ+R sin θ y_E =4R cos θ I_E =I+m(x_E −x_G )^2 +m(y_E −y_G )^2 =((m(4R^2 +16R^2 ))/(12))+m(−2 sin θ+cos θ)^2 R^2 +m(−2 cos θ+sin θ)^2 R^2 =(((20−12 sin 2θ)mR^2 )/3) ((I_E ω^2 )/2)+((mv_B ^2 )/2)=mg((√5)R−y_G ) ((I_E ω^2 )/2)+((mv_B ^2 )/2)=mgR((√5)−2 cos θ−sin θ) (((20−12 sin 2θ)mω^2 R^2 )/6)+((4mR^2 (2cos θ−sin θ−cos θ tan ϕ)^2 ω^2 )/2)=mgR((√5)−2 cos θ−sin θ) [10−6 sin 2θ+6(2cos θ−sin θ−cos θ tan ϕ)^2 ]ω^2 =((3g)/R)((√5)−2 cos θ−sin θ) ω^2 =((3g)/R)×(((√5)−2 cos θ−sin θ)/(10−6 sin 2θ+6(2cos θ−sin θ−cos θ tan ϕ)^2 )) ω=(√((3g)/R))×f(θ) with f(θ)=(√(((√5)−2 cos θ−sin θ)/(10−6 sin 2θ+6(2cos θ−sin θ−cos θ tan ϕ)^2 ))) we get from (I) θ≈0.7296≈41.8° at which N=0 all above is valid for tan^(−1) (1/2)≤θ≤θ_(max) ϕ+θ_(max) =90° sin (90°−θ_(max) )=2 sin θ_(max) −1 2 sin θ_(max) −cos θ_(max) =1 sin (θ_(max) −tan^(−1) (1/2))=(1/( (√5))) θ_(max) =sin^(−1) (1/( (√5)))+tan^(−1) (1/2)≈53.1° N=0 occours at θ≈41.8°, before θ_(max) is reached.](https://www.tinkutara.com/question/Q159224.png)
$$\mathrm{2}{R}\mathrm{sin}\:\theta={R}+{R}\mathrm{sin}\:\varphi \\ $$$$\mathrm{sin}\:\varphi=\mathrm{2}\:\mathrm{sin}\:\theta−\mathrm{1} \\ $$$$\frac{{d}\varphi}{{d}\theta}=\frac{\mathrm{2}\:\mathrm{cos}\:\theta}{\mathrm{cos}\:\varphi}=\frac{\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}} \\ $$$${x}_{{A}} ={x}_{{E}} =\mathrm{4}{R}\:\mathrm{sin}\:\theta \\ $$$${x}_{{B}} ={x}_{{A}} +\mathrm{2}{R}\:\mathrm{cos}\:\theta+{R}\:\mathrm{cos}\:\varphi \\ $$$${x}_{{B}} =\mathrm{4}{R}\:\mathrm{sin}\:\theta+\mathrm{2}{R}\:\mathrm{cos}\:\theta+{R}\:\mathrm{cos}\:\varphi \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${v}_{{B}} =\frac{{dx}_{{B}} }{{dt}}=\mathrm{4}{R}\mathrm{cos}\:\theta\:\omega−\mathrm{2}{R}\:\mathrm{sin}\:\theta\:\omega−{R}\:\mathrm{sin}\:\varphi\:\omega\:\frac{{d}\varphi}{{d}\theta} \\ $$$${v}_{{B}} =\mathrm{2}{R}\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)\omega \\ $$$$\frac{{dv}_{{B}} }{{d}\theta}=\mathrm{2}{R}\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)\frac{{d}\omega}{{d}\theta} \\ $$$$+\mathrm{2}{R}\omega\left(−\mathrm{2sin}\:\theta−\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\mathrm{tan}\:\varphi−\frac{\mathrm{2cos}^{\mathrm{2}} \:\theta}{\mathrm{cos}^{\mathrm{3}} \:\varphi}\right) \\ $$$${a}_{{B}} =\frac{{dv}_{{B}} }{{dt}}=\omega\frac{{dv}_{{B}} }{{d}\theta} \\ $$$$=\mathrm{2}{R}\omega\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)\frac{{d}\omega}{{d}\theta} \\ $$$$+\mathrm{2}{R}\omega^{\mathrm{2}} \left(−\mathrm{2sin}\:\theta−\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\mathrm{tan}\:\varphi−\frac{\mathrm{2cos}^{\mathrm{2}} \:\theta}{\mathrm{cos}^{\mathrm{3}} \:\varphi}\right) \\ $$$${N}\mathrm{cos}\:\varphi={ma}_{{B}} \\ $$$${N}=\mathrm{0}\:\Rightarrow{a}_{{B}} =\mathrm{0} \\ $$$$\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)\frac{{d}\omega}{{d}\theta} \\ $$$$−\omega\left(\mathrm{2sin}\:\theta+\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\:\mathrm{tan}\:\varphi+\frac{\mathrm{2cos}^{\mathrm{2}} \:\theta}{\mathrm{cos}^{\mathrm{3}} \:\varphi}\right)=\mathrm{0}\:\:\:..\left({I}\right) \\ $$$$ \\ $$$${x}_{{G}} −{x}_{{A}} =\left(−\mathrm{2sin}\:\theta+\mathrm{cos}\:\theta\right){R} \\ $$$${y}_{{G}} =\mathrm{2}{R}\:\mathrm{cos}\:\theta+{R}\:\mathrm{sin}\:\theta \\ $$$${y}_{{E}} =\mathrm{4}{R}\:\mathrm{cos}\:\theta \\ $$$${I}_{{E}} ={I}+{m}\left({x}_{{E}} −{x}_{{G}} \right)^{\mathrm{2}} +{m}\left({y}_{{E}} −{y}_{{G}} \right)^{\mathrm{2}} \\ $$$$=\frac{{m}\left(\mathrm{4}{R}^{\mathrm{2}} +\mathrm{16}{R}^{\mathrm{2}} \right)}{\mathrm{12}}+{m}\left(−\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} {R}^{\mathrm{2}} +{m}\left(−\mathrm{2}\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)^{\mathrm{2}} {R}^{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{20}−\mathrm{12}\:\mathrm{sin}\:\mathrm{2}\theta\right){mR}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\frac{{I}_{{E}} \omega^{\mathrm{2}} }{\mathrm{2}}+\frac{{mv}_{{B}} ^{\mathrm{2}} }{\mathrm{2}}={mg}\left(\sqrt{\mathrm{5}}{R}−{y}_{{G}} \right) \\ $$$$\frac{{I}_{{E}} \omega^{\mathrm{2}} }{\mathrm{2}}+\frac{{mv}_{{B}} ^{\mathrm{2}} }{\mathrm{2}}={mgR}\left(\sqrt{\mathrm{5}}−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$$$\frac{\left(\mathrm{20}−\mathrm{12}\:\mathrm{sin}\:\mathrm{2}\theta\right){m}\omega^{\mathrm{2}} {R}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{4}{mR}^{\mathrm{2}} \left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{2}}={mgR}\left(\sqrt{\mathrm{5}}−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$$$\left[\mathrm{10}−\mathrm{6}\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{6}\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)^{\mathrm{2}} \right]\omega^{\mathrm{2}} =\frac{\mathrm{3}{g}}{{R}}\left(\sqrt{\mathrm{5}}−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{3}{g}}{{R}}×\frac{\sqrt{\mathrm{5}}−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta}{\mathrm{10}−\mathrm{6}\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{6}\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)^{\mathrm{2}} } \\ $$$$\omega=\sqrt{\frac{\mathrm{3}{g}}{{R}}}×{f}\left(\theta\right) \\ $$$${with}\:{f}\left(\theta\right)=\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta}{\mathrm{10}−\mathrm{6}\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{6}\left(\mathrm{2cos}\:\theta−\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\:\mathrm{tan}\:\varphi\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$${we}\:{get}\:{from}\:\left({I}\right) \\ $$$$\theta\approx\mathrm{0}.\mathrm{7296}\approx\mathrm{41}.\mathrm{8}°\:{at}\:{which}\:{N}=\mathrm{0} \\ $$$$ \\ $$$${all}\:{above}\:{is}\:{valid}\:{for}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\leqslant\theta\leqslant\theta_{{max}} \\ $$$$\varphi+\theta_{{max}} =\mathrm{90}° \\ $$$$\mathrm{sin}\:\left(\mathrm{90}°−\theta_{{max}} \right)=\mathrm{2}\:\mathrm{sin}\:\theta_{{max}} −\mathrm{1} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\theta_{{max}} −\mathrm{cos}\:\theta_{{max}} =\mathrm{1} \\ $$$$\mathrm{sin}\:\left(\theta_{{max}} −\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\theta_{{max}} =\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\approx\mathrm{53}.\mathrm{1}° \\ $$$${N}=\mathrm{0}\:{occours}\:{at}\:\theta\approx\mathrm{41}.\mathrm{8}°,\:{before} \\ $$$$\theta_{{max}} \:{is}\:{reached}. \\ $$
Commented by mr W last updated on 14/Nov/21
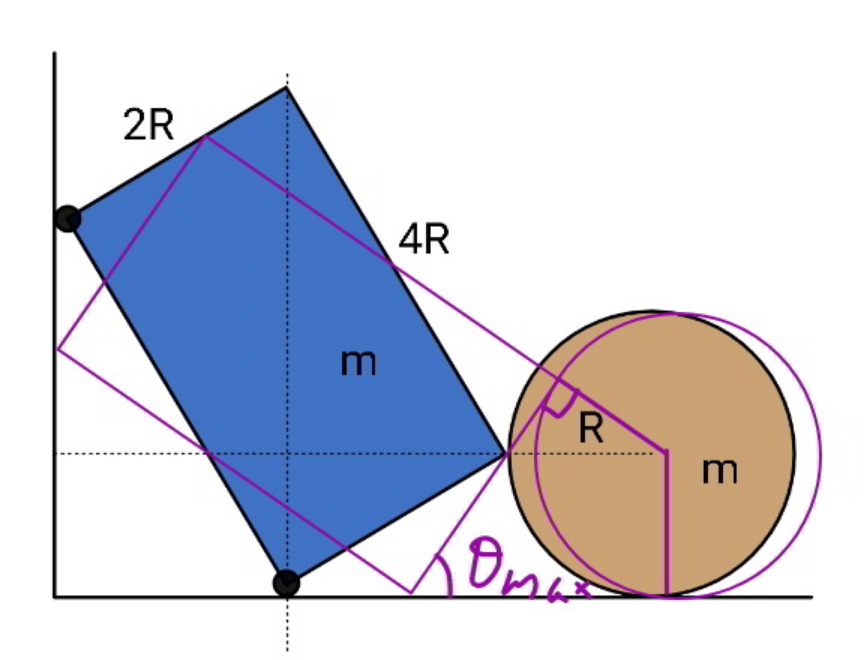
Commented by mr W last updated on 18/Nov/21
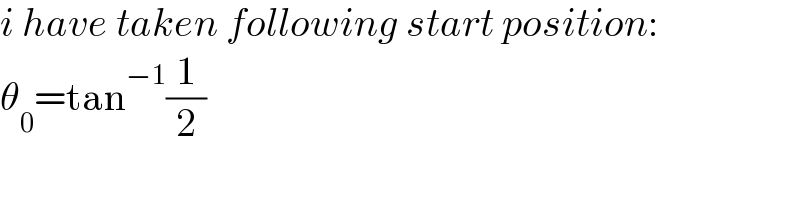
$${i}\:{have}\:{taken}\:{following}\:{start}\:{position}: \\ $$$$\theta_{\mathrm{0}} =\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 14/Nov/21