Question Number 159143 by mnjuly1970 last updated on 13/Nov/21

Answered by qaz last updated on 14/Nov/21
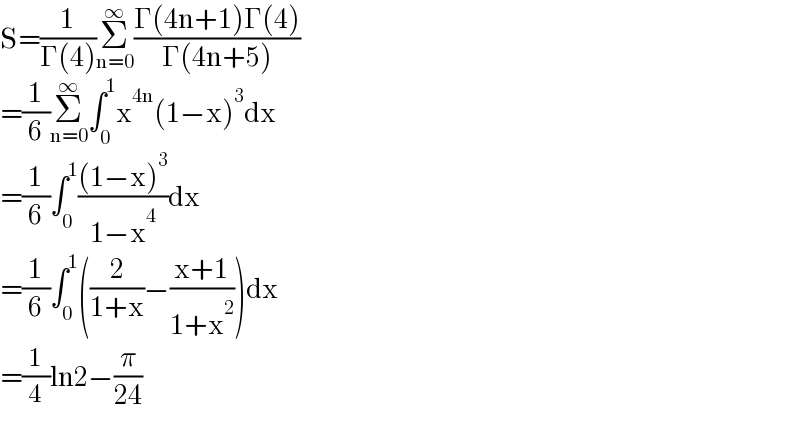
$$\mathrm{S}=\frac{\mathrm{1}}{\Gamma\left(\mathrm{4}\right)}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma\left(\mathrm{4n}+\mathrm{1}\right)\Gamma\left(\mathrm{4}\right)}{\Gamma\left(\mathrm{4n}+\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{4n}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{x}}−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln2}−\frac{\pi}{\mathrm{24}} \\ $$
Commented by mnjuly1970 last updated on 14/Nov/21

$${bravo}\:{mr}\:{qaz} \\ $$
Commented by ArielVyny last updated on 14/Nov/21

$${mr}\:{qaz}\:{je}\:{peux}\:{avoir}\:{la}\:{forme}\:{general}\:{de} \\ $$$${ce}\:{genre}\:{d}'{expression}? \\ $$
