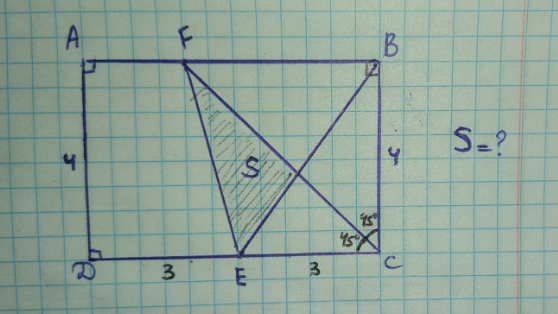
Question Number 159396 by quvonnn last updated on 16/Nov/21
Answered by som(math1967) last updated on 16/Nov/21
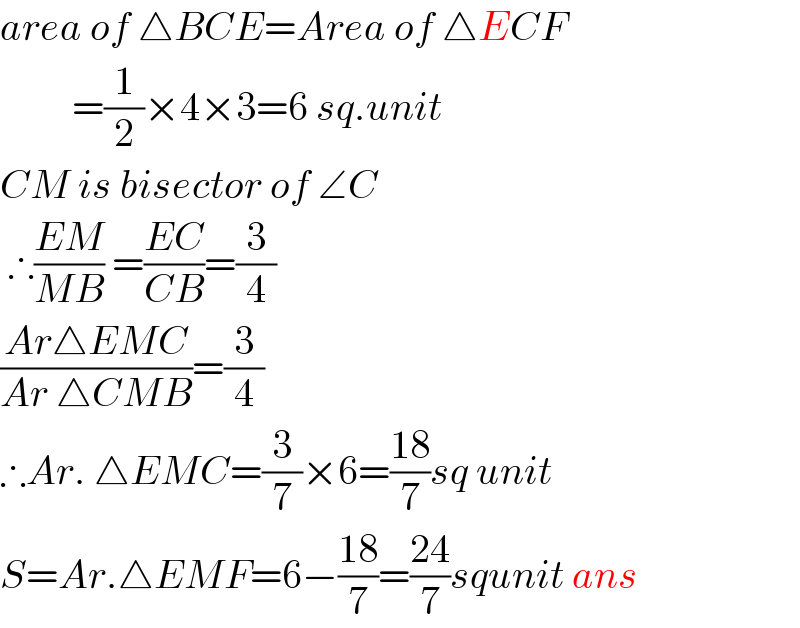
$${area}\:{of}\:\bigtriangleup{BCE}={Area}\:{of}\:\bigtriangleup{ECF} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}×\mathrm{3}=\mathrm{6}\:{sq}.{unit} \\ $$$${CM}\:{is}\:{bisector}\:{of}\:\angle{C} \\ $$$$\:\therefore\frac{{EM}}{{MB}}\:=\frac{{EC}}{{CB}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{Ar}\bigtriangleup{EMC}}{{Ar}\:\bigtriangleup{CMB}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\therefore{Ar}.\:\bigtriangleup{EMC}=\frac{\mathrm{3}}{\mathrm{7}}×\mathrm{6}=\frac{\mathrm{18}}{\mathrm{7}}{sq}\:{unit} \\ $$$${S}={Ar}.\bigtriangleup{EMF}=\mathrm{6}−\frac{\mathrm{18}}{\mathrm{7}}=\frac{\mathrm{24}}{\mathrm{7}}{squnit}\:{ans} \\ $$
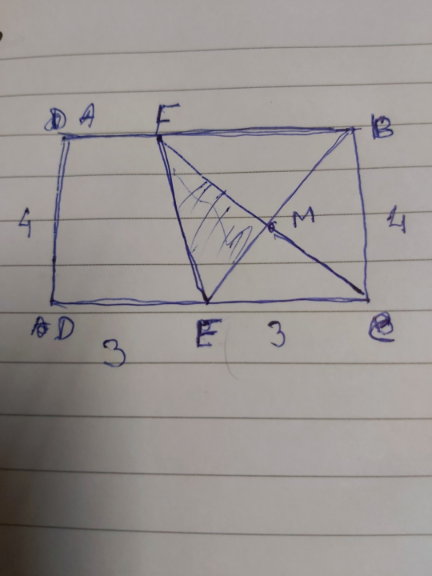
Commented by som(math1967) last updated on 16/Nov/21
Commented by Rasheed.Sindhi last updated on 16/Nov/21
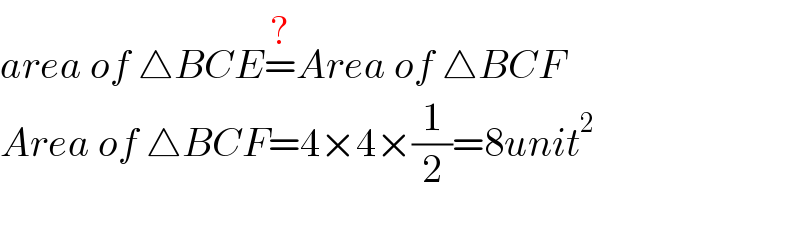
$${area}\:{of}\:\bigtriangleup{BCE}\overset{?} {=}{Area}\:{of}\:\bigtriangleup{BCF} \\ $$$${Area}\:{of}\:\bigtriangleup{BCF}=\mathrm{4}×\mathrm{4}×\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{8}{unit}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 16/Nov/21
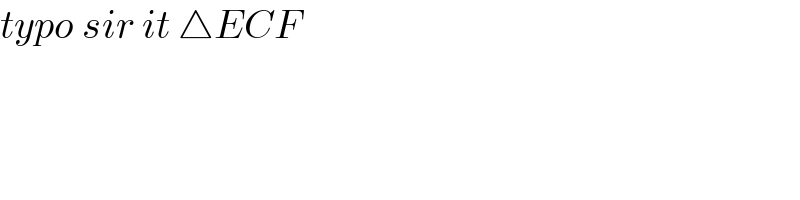
$${typo}\:{sir}\:{it}\:\bigtriangleup{ECF} \\ $$
Commented by Avijit007 last updated on 16/Nov/21

$${yes}. \\ $$
