Question Number 159472 by mnjuly1970 last updated on 17/Nov/21

Answered by MJS_new last updated on 18/Nov/21
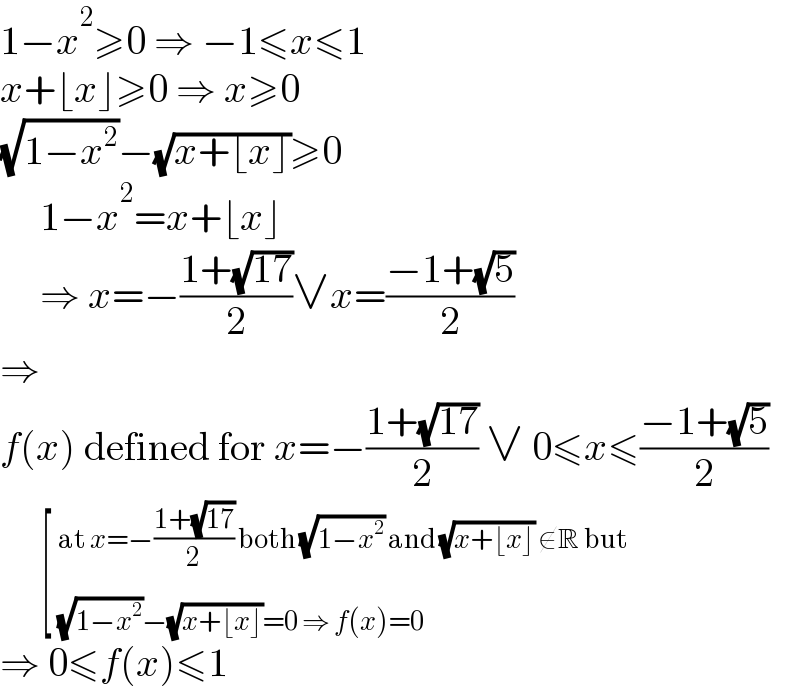
$$\mathrm{1}−{x}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$${x}+\lfloor{x}\rfloor\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant\mathrm{0} \\ $$$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\sqrt{{x}+\lfloor{x}\rfloor}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{1}−{x}^{\mathrm{2}} ={x}+\lfloor{x}\rfloor \\ $$$$\:\:\:\:\:\Rightarrow\:{x}=−\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}\vee{x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)\:\mathrm{defined}\:\mathrm{for}\:{x}=−\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}\:\vee\:\mathrm{0}\leqslant{x}\leqslant\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\left[\:_{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\sqrt{{x}+\lfloor{x}\rfloor}=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{0}} ^{\mathrm{at}\:{x}=−\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}\:\mathrm{both}\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{and}\:\sqrt{{x}+\lfloor{x}\rfloor}\:\notin\mathbb{R}\:\mathrm{but}} \right. \\ $$$$\Rightarrow\:\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 19/Nov/21
$${mercey}\:{master}\:{thank}\:{you}\:{so}\:{much} \\ $$
