Question Number 159612 by cortano last updated on 19/Nov/21
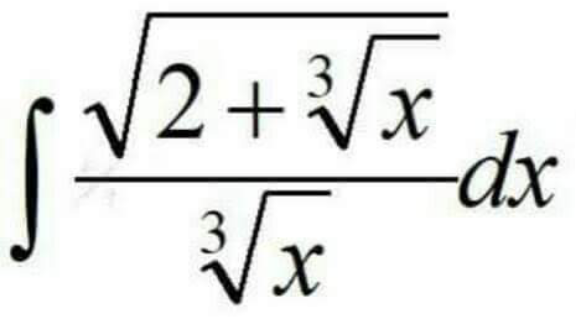
Answered by Ar Brandon last updated on 19/Nov/21
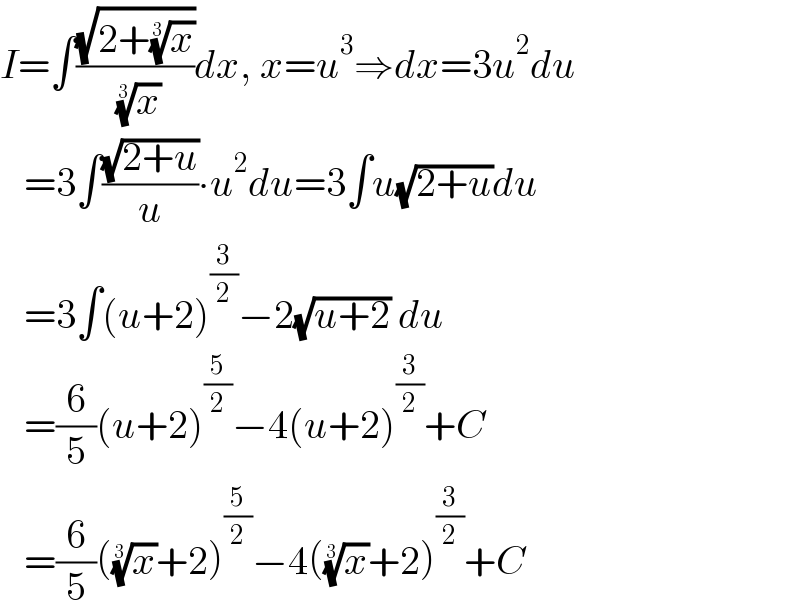
$${I}=\int\frac{\sqrt{\mathrm{2}+\sqrt[{\mathrm{3}}]{{x}}}}{\:\sqrt[{\mathrm{3}}]{{x}}}{dx},\:{x}={u}^{\mathrm{3}} \Rightarrow{dx}=\mathrm{3}{u}^{\mathrm{2}} {du} \\ $$$$\:\:\:=\mathrm{3}\int\frac{\sqrt{\mathrm{2}+{u}}}{{u}}\centerdot{u}^{\mathrm{2}} {du}=\mathrm{3}\int{u}\sqrt{\mathrm{2}+{u}}{du} \\ $$$$\:\:\:=\mathrm{3}\int\left({u}+\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{2}\sqrt{{u}+\mathrm{2}}\:{du} \\ $$$$\:\:\:=\frac{\mathrm{6}}{\mathrm{5}}\left({u}+\mathrm{2}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{4}\left({u}+\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$$$\:\:\:=\frac{\mathrm{6}}{\mathrm{5}}\left(\sqrt[{\mathrm{3}}]{{x}}+\mathrm{2}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{4}\left(\sqrt[{\mathrm{3}}]{{x}}+\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$
Answered by tounghoungko last updated on 19/Nov/21
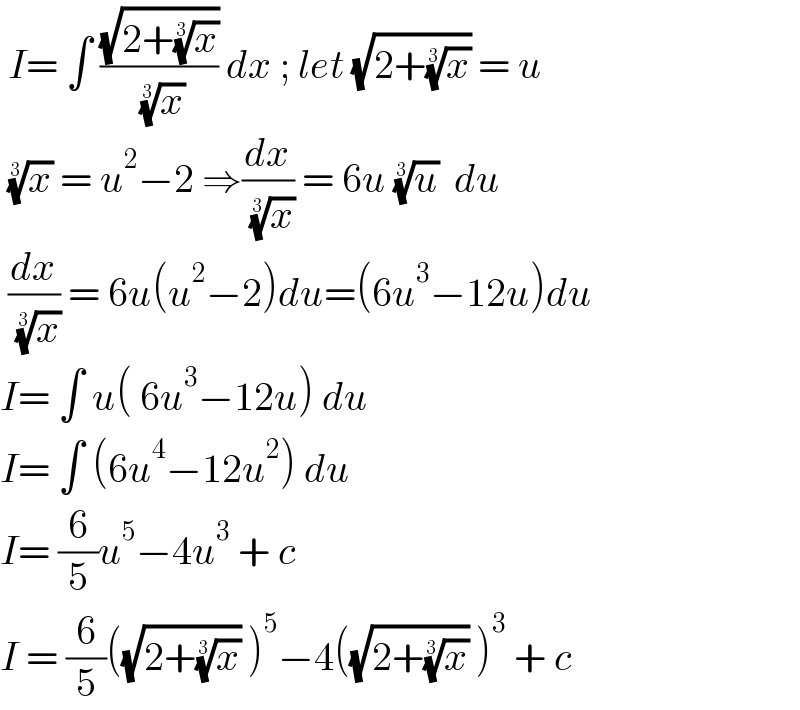
$$\:{I}=\:\int\:\frac{\sqrt{\mathrm{2}+\sqrt[{\mathrm{3}}]{{x}}}}{\:\sqrt[{\mathrm{3}}]{{x}}}\:{dx}\:;\:{let}\:\sqrt{\mathrm{2}+\sqrt[{\mathrm{3}}]{{x}}}\:=\:{u}\: \\ $$$$\:\sqrt[{\mathrm{3}}]{{x}}\:=\:{u}^{\mathrm{2}} −\mathrm{2}\:\Rightarrow\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}}\:=\:\mathrm{6}{u}\:\sqrt[{\mathrm{3}}]{{u}}\:\:{du} \\ $$$$\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}}\:=\:\mathrm{6}{u}\left({u}^{\mathrm{2}} −\mathrm{2}\right){du}=\left(\mathrm{6}{u}^{\mathrm{3}} −\mathrm{12}{u}\right){du}\: \\ $$$${I}=\:\int\:{u}\left(\:\mathrm{6}{u}^{\mathrm{3}} −\mathrm{12}{u}\right)\:{du} \\ $$$${I}=\:\int\:\left(\mathrm{6}{u}^{\mathrm{4}} −\mathrm{12}{u}^{\mathrm{2}} \right)\:{du} \\ $$$${I}=\:\frac{\mathrm{6}}{\mathrm{5}}{u}^{\mathrm{5}} −\mathrm{4}{u}^{\mathrm{3}} \:+\:{c} \\ $$$${I}\:=\:\frac{\mathrm{6}}{\mathrm{5}}\left(\sqrt{\mathrm{2}+\sqrt[{\mathrm{3}}]{{x}}}\:\right)^{\mathrm{5}} −\mathrm{4}\left(\sqrt{\mathrm{2}+\sqrt[{\mathrm{3}}]{{x}}}\:\right)^{\mathrm{3}} \:+\:{c}\: \\ $$
