Question Number 159675 by Tawa11 last updated on 19/Nov/21
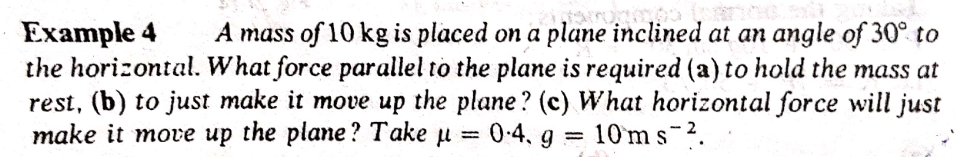
Commented by mr W last updated on 20/Nov/21
$${i}\:{remember}\:{this}\:{question}\:{is}\:{not}\:{asked} \\ $$$${for}\:{the}\:{first}\:{time}. \\ $$
Commented by Tawa11 last updated on 20/Nov/21

$$\mathrm{Wow},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}. \\ $$
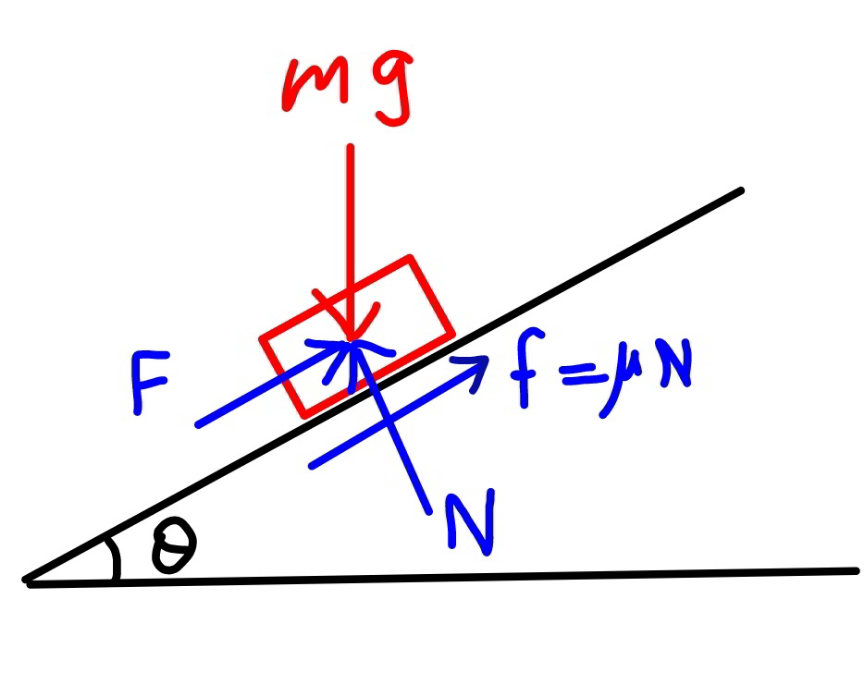
Answered by mr W last updated on 20/Nov/21
Commented by mr W last updated on 20/Nov/21
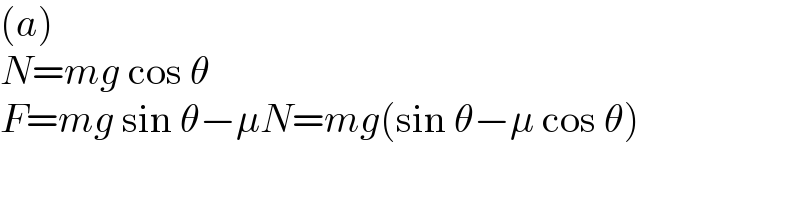
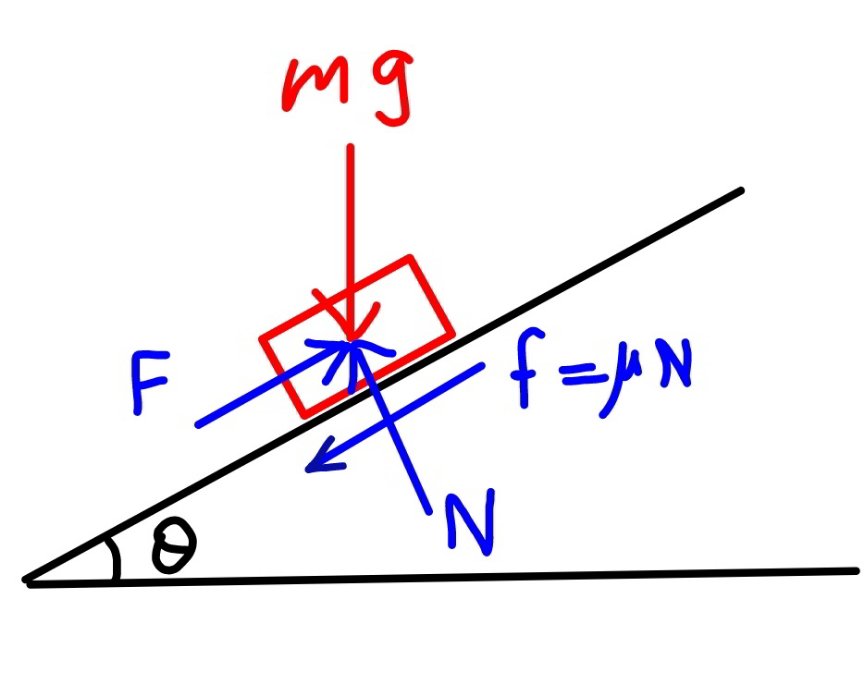
$$\left({a}\right) \\ $$$${N}={mg}\:\mathrm{cos}\:\theta \\ $$$${F}={mg}\:\mathrm{sin}\:\theta−\mu{N}={mg}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right) \\ $$
Commented by mr W last updated on 20/Nov/21
Commented by mr W last updated on 20/Nov/21
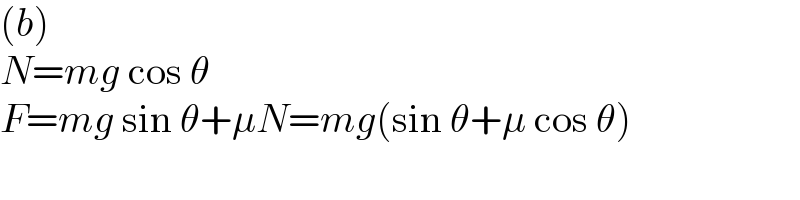
$$\left({b}\right) \\ $$$${N}={mg}\:\mathrm{cos}\:\theta \\ $$$${F}={mg}\:\mathrm{sin}\:\theta+\mu{N}={mg}\left(\mathrm{sin}\:\theta+\mu\:\mathrm{cos}\:\theta\right) \\ $$
Commented by mr W last updated on 20/Nov/21
Commented by mr W last updated on 20/Nov/21
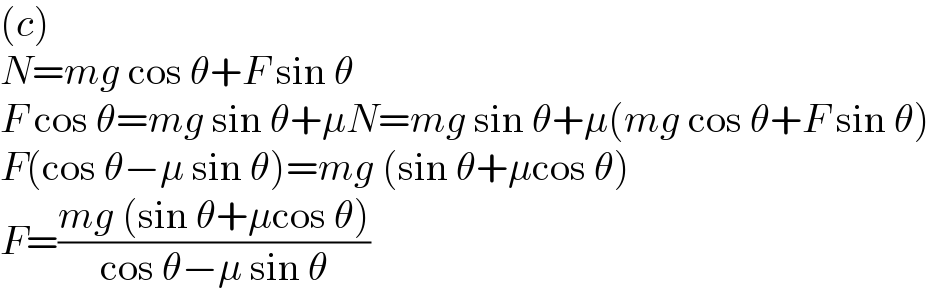
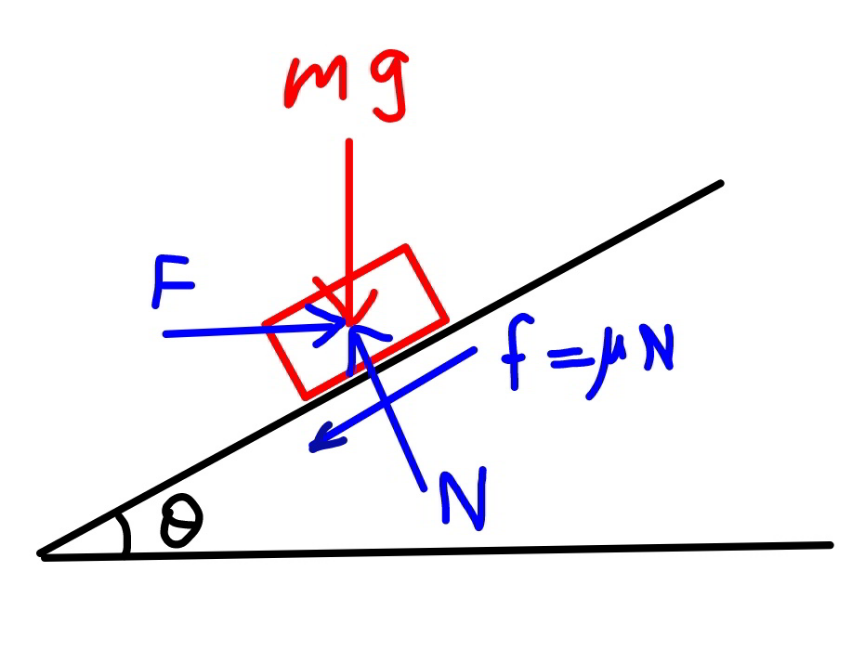
$$\left({c}\right) \\ $$$${N}={mg}\:\mathrm{cos}\:\theta+{F}\:\mathrm{sin}\:\theta \\ $$$${F}\:\mathrm{cos}\:\theta={mg}\:\mathrm{sin}\:\theta+\mu{N}={mg}\:\mathrm{sin}\:\theta+\mu\left({mg}\:\mathrm{cos}\:\theta+{F}\:\mathrm{sin}\:\theta\right) \\ $$$${F}\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right)={mg}\:\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right) \\ $$$${F}=\frac{{mg}\:\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)}{\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta} \\ $$
Commented by mr W last updated on 20/Nov/21
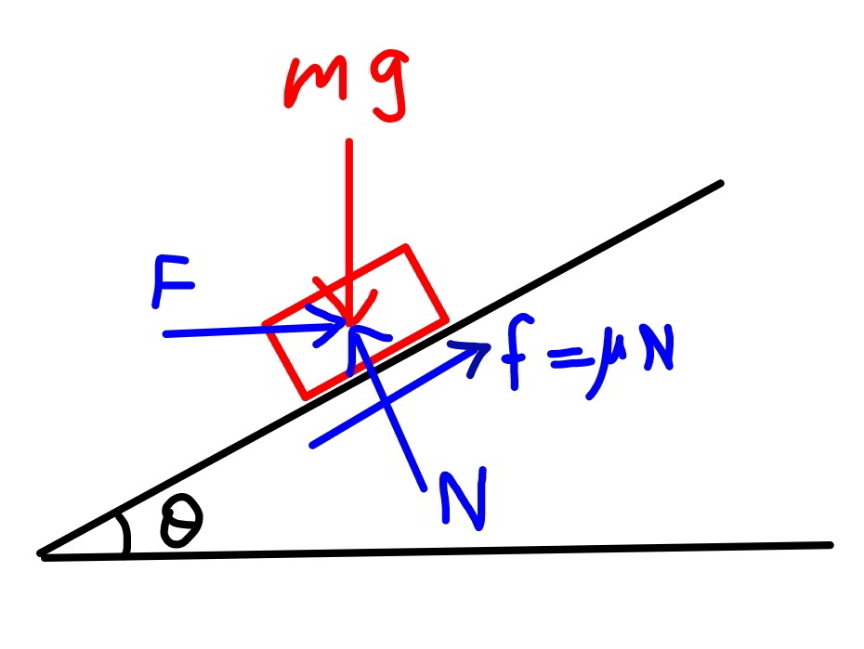
Commented by mr W last updated on 20/Nov/21
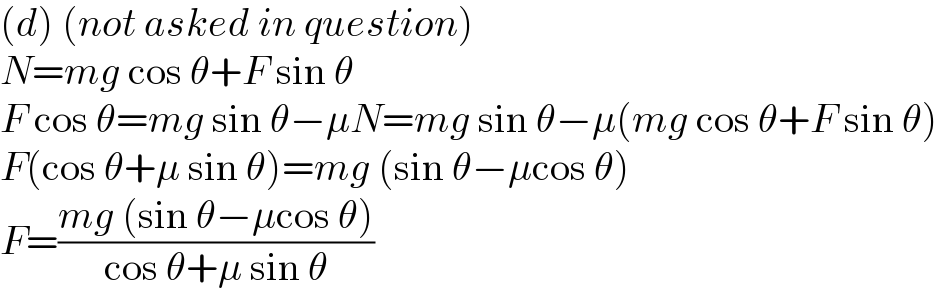
$$\left({d}\right)\:\left({not}\:{asked}\:{in}\:{question}\right) \\ $$$${N}={mg}\:\mathrm{cos}\:\theta+{F}\:\mathrm{sin}\:\theta \\ $$$${F}\:\mathrm{cos}\:\theta={mg}\:\mathrm{sin}\:\theta−\mu{N}={mg}\:\mathrm{sin}\:\theta−\mu\left({mg}\:\mathrm{cos}\:\theta+{F}\:\mathrm{sin}\:\theta\right) \\ $$$${F}\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)={mg}\:\left(\mathrm{sin}\:\theta−\mu\mathrm{cos}\:\theta\right) \\ $$$${F}=\frac{{mg}\:\left(\mathrm{sin}\:\theta−\mu\mathrm{cos}\:\theta\right)}{\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta} \\ $$
