Question Number 159748 by 07814040830 last updated on 20/Nov/21
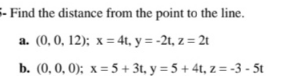
Answered by 07814040830 last updated on 20/Nov/21

$$ \\ $$
Answered by TheSupreme last updated on 21/Nov/21
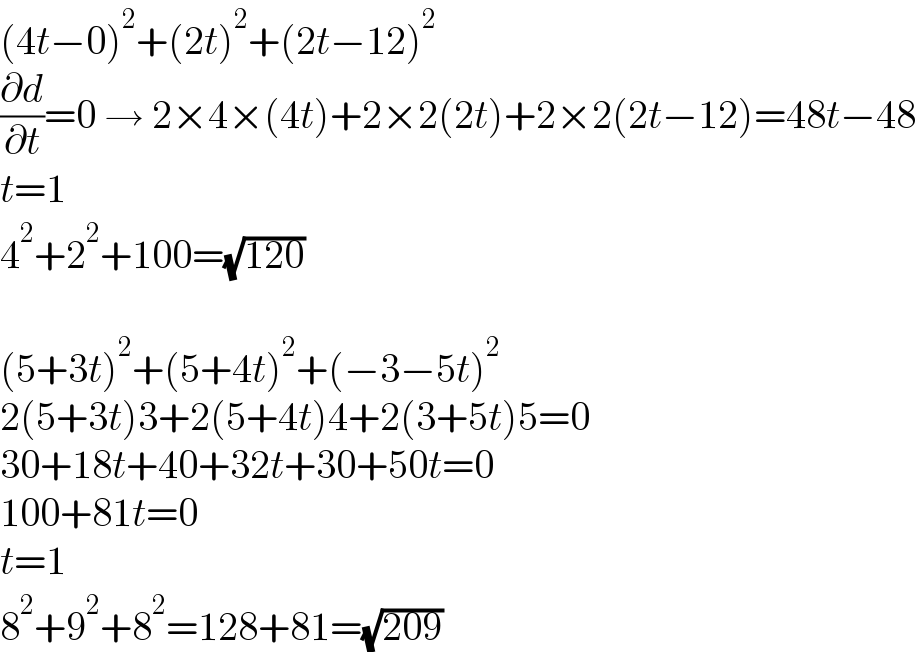
$$\left(\mathrm{4}{t}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{2}{t}\right)^{\mathrm{2}} +\left(\mathrm{2}{t}−\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\frac{\partial{d}}{\partial{t}}=\mathrm{0}\:\rightarrow\:\mathrm{2}×\mathrm{4}×\left(\mathrm{4}{t}\right)+\mathrm{2}×\mathrm{2}\left(\mathrm{2}{t}\right)+\mathrm{2}×\mathrm{2}\left(\mathrm{2}{t}−\mathrm{12}\right)=\mathrm{48}{t}−\mathrm{48} \\ $$$${t}=\mathrm{1} \\ $$$$\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{100}=\sqrt{\mathrm{120}} \\ $$$$ \\ $$$$\left(\mathrm{5}+\mathrm{3}{t}\right)^{\mathrm{2}} +\left(\mathrm{5}+\mathrm{4}{t}\right)^{\mathrm{2}} +\left(−\mathrm{3}−\mathrm{5}{t}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{5}+\mathrm{3}{t}\right)\mathrm{3}+\mathrm{2}\left(\mathrm{5}+\mathrm{4}{t}\right)\mathrm{4}+\mathrm{2}\left(\mathrm{3}+\mathrm{5}{t}\right)\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{30}+\mathrm{18}{t}+\mathrm{40}+\mathrm{32}{t}+\mathrm{30}+\mathrm{50}{t}=\mathrm{0} \\ $$$$\mathrm{100}+\mathrm{81}{t}=\mathrm{0} \\ $$$${t}=\mathrm{1} \\ $$$$\mathrm{8}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} =\mathrm{128}+\mathrm{81}=\sqrt{\mathrm{209}} \\ $$
