Question Number 15982 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 17/Jun/17
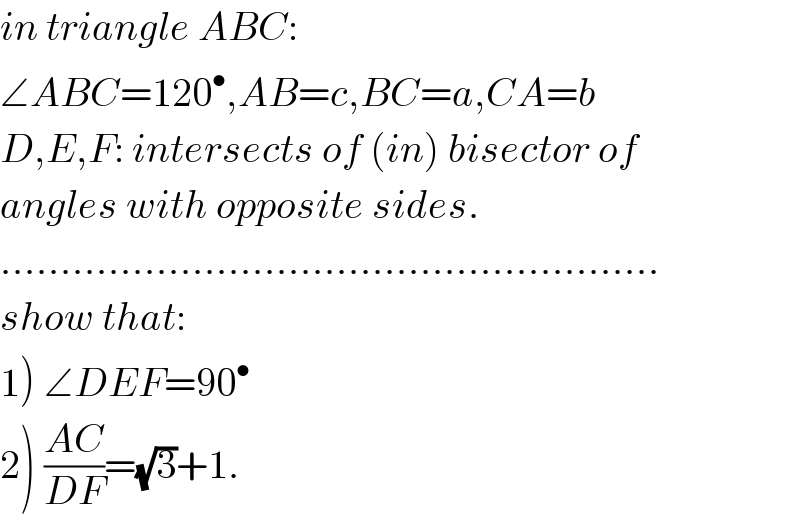
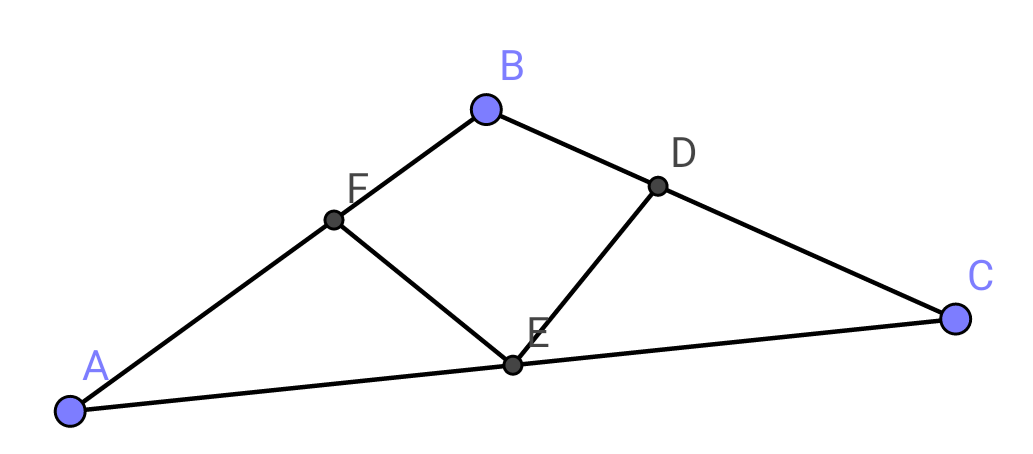
$${in}\:{triangle}\:{ABC}: \\ $$$$\angle{ABC}=\mathrm{120}^{\bullet} ,{AB}={c},{BC}={a},{CA}={b} \\ $$$${D},{E},{F}:\:{intersects}\:{of}\:\left({in}\right)\:{bisector}\:{of} \\ $$$${angles}\:{with}\:{opposite}\:{sides}. \\ $$$$………………………………………………. \\ $$$${show}\:{that}: \\ $$$$\left.\mathrm{1}\right)\:\angle{DEF}=\mathrm{90}^{\bullet} \\ $$$$\left.\mathrm{2}\right)\:\frac{{AC}}{{DF}}=\sqrt{\mathrm{3}}+\mathrm{1}. \\ $$
Commented by ajfour last updated on 16/Jun/17

$${some}\:{more}\:{explanation}\:{about} \\ $$$${these}\:{inbisectors}.. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17
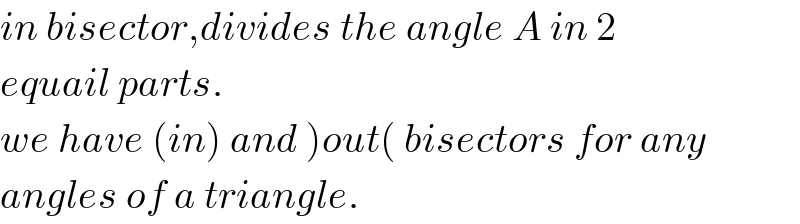
$${in}\:{bisector},{divides}\:{the}\:{angle}\:{A}\:{in}\:\mathrm{2}\: \\ $$$${equail}\:{parts}. \\ $$$$\left.{we}\:{have}\:\left({in}\right)\:{and}\:\right){out}\left(\:{bisectors}\:{for}\:{any}\right. \\ $$$${angles}\:{of}\:{a}\:{triangle}. \\ $$
