Menu Close

Question-159852

Tinku Tara 0 Comments
Pin




Question Number 159852 by Tawa11 last updated on 21/Nov/21
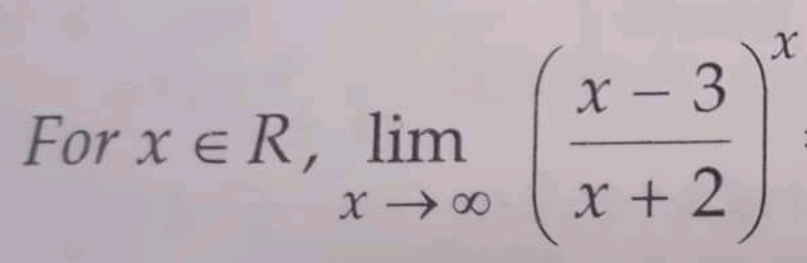
Answered by tounghoungko last updated on 21/Nov/21
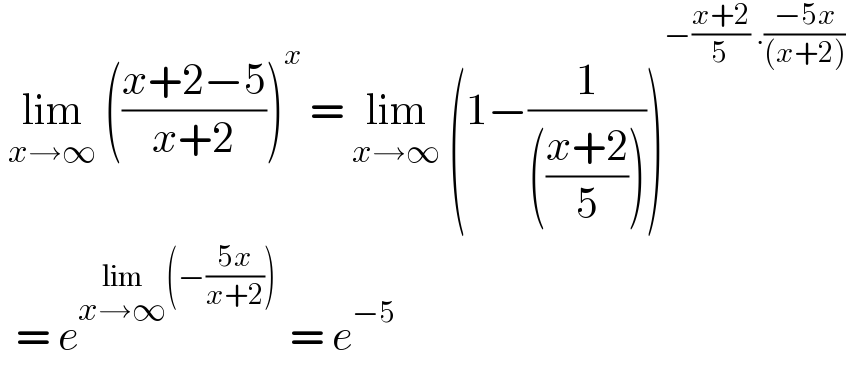
lim_(x→∞) (((x+2−5)/(x+2)))^x = lim_(x→∞) (1−(1/((((x+2)/5)))))^(−((x+2)/5) .((−5x)/((x+2)))) = e^(lim_(x→∞) (−((5x)/(x+2))) ) = e^(−5)
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}+\mathrm{2}−\mathrm{5}}{{x}+\mathrm{2}}\right)^{{x}} \:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\left(\frac{{x}+\mathrm{2}}{\mathrm{5}}\right)}\right)^{−\frac{{x}+\mathrm{2}}{\mathrm{5}}\:.\frac{−\mathrm{5}{x}}{\left({x}+\mathrm{2}\right)}} \\ $$$$\:\:=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(−\frac{\mathrm{5}{x}}{{x}+\mathrm{2}}\right)\:} \:=\:{e}^{−\mathrm{5}} \: \\ $$
Commented by Tawa11 last updated on 21/Nov/21
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by LEKOUMA last updated on 21/Nov/21
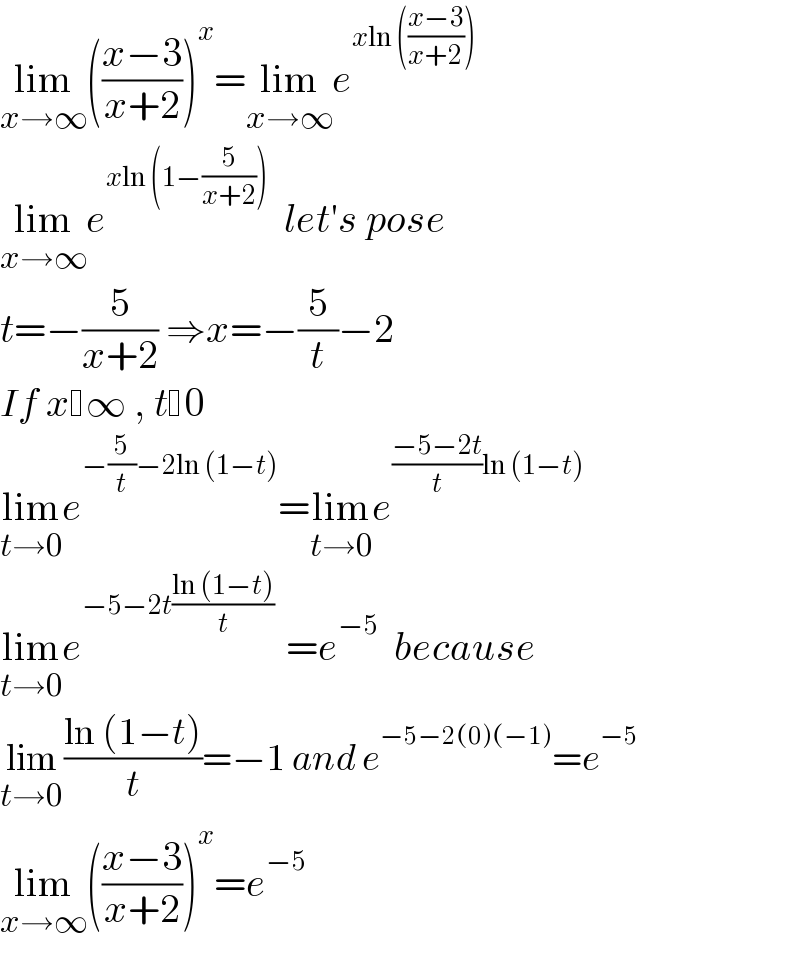
lim_(x→∞) (((x−3)/(x+2)))^x =lim_(x→∞) e^(xln (((x−3)/(x+2)))) lim_(x→∞) e^(xln (1−(5/(x+2)))) let′s pose t=−(5/(x+2)) ⇒x=−(5/t)−2 If x ∞ , t 0 lim_(t→0) e^(−(5/t)−2ln (1−t)) =lim_(t→0) e^(((−5−2t)/t)ln (1−t)) lim_(t→0) e^(−5−2t((ln (1−t))/t) ) =e^(−5) because lim_(t→0) ((ln (1−t))/t)=−1 and e^(−5−2(0)(−1)) =e^(−5) lim_(x→∞) (((x−3)/(x+2)))^x =e^(−5)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{2}}\right)^{{x}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}{e}^{{x}\mathrm{ln}\:\left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{2}}\right)} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{e}^{{x}\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{5}}{{x}+\mathrm{2}}\right)} \:\:{let}'{s}\:{pose}\: \\ $$$${t}=−\frac{\mathrm{5}}{{x}+\mathrm{2}}\:\Rightarrow{x}=−\frac{\mathrm{5}}{{t}}−\mathrm{2}\: \\ $$$${If}\:{x} \infty\:,\:{t} \mathrm{0}\: \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{−\frac{\mathrm{5}}{{t}}−\mathrm{2ln}\:\left(\mathrm{1}−{t}\right)} =\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{\frac{−\mathrm{5}−\mathrm{2}{t}}{{t}}\mathrm{ln}\:\left(\mathrm{1}−{t}\right)} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{−\mathrm{5}−\mathrm{2}{t}\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{{t}}\:} \:={e}^{−\mathrm{5}} \:\:{because}\: \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{{t}}=−\mathrm{1}\:{and}\:{e}^{−\mathrm{5}−\mathrm{2}\left(\mathrm{0}\right)\left(−\mathrm{1}\right)} ={e}^{−\mathrm{5}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{2}}\right)^{{x}} ={e}^{−\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *