Question Number 15993 by ajfour last updated on 16/Jun/17
Commented by ajfour last updated on 16/Jun/17

$$\:{answer}\:{to}\:{Q}.\mathrm{15969}\: \\ $$
Answered by ajfour last updated on 19/Jun/17
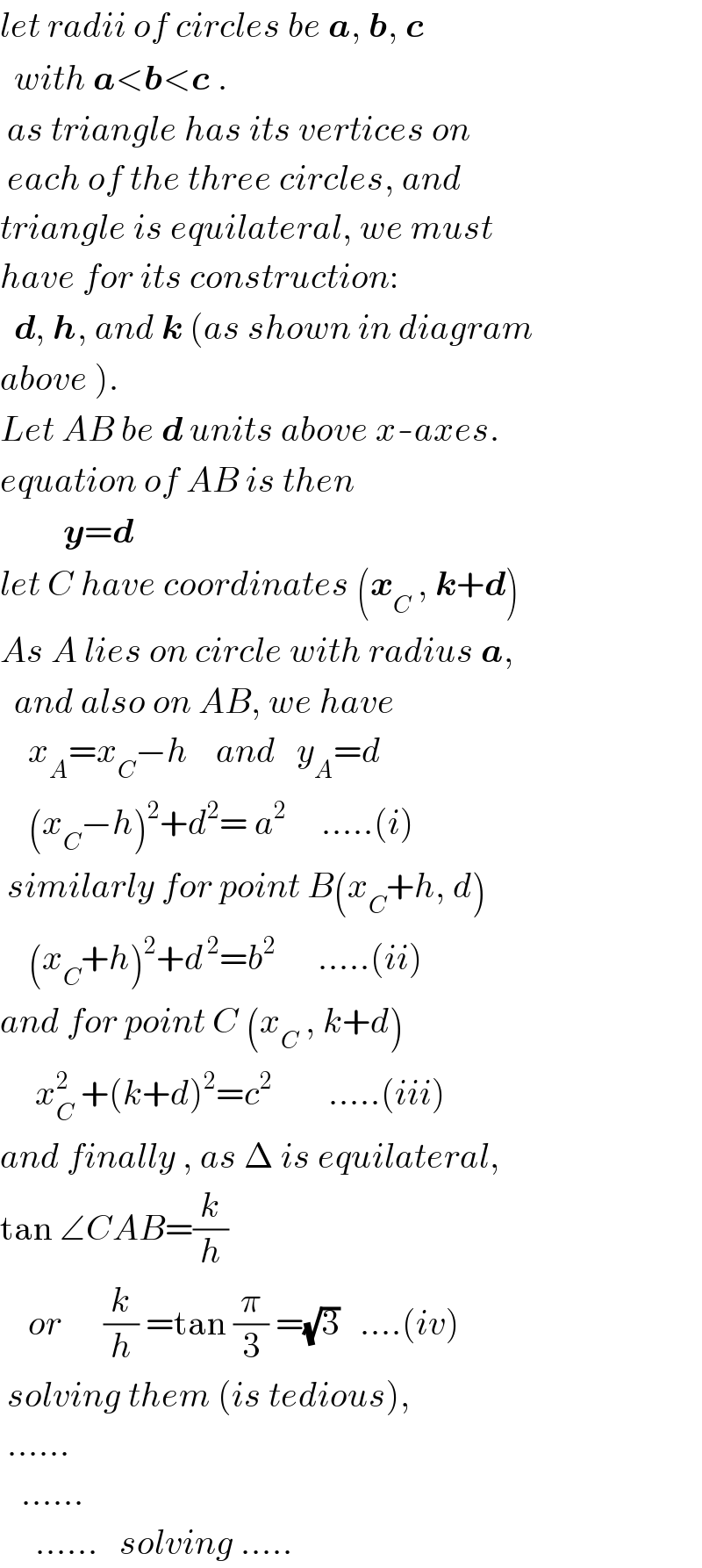
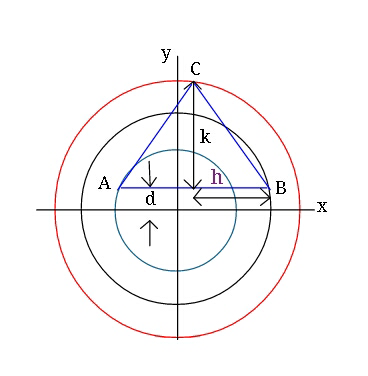
$${let}\:{radii}\:{of}\:{circles}\:{be}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}} \\ $$$$\:\:{with}\:\boldsymbol{{a}}<\boldsymbol{{b}}<\boldsymbol{{c}}\:. \\ $$$$\:{as}\:{triangle}\:{has}\:{its}\:{vertices}\:{on} \\ $$$$\:{each}\:{of}\:{the}\:{three}\:{circles},\:{and} \\ $$$${triangle}\:{is}\:{equilateral},\:{we}\:{must} \\ $$$${have}\:{for}\:{its}\:{construction}: \\ $$$$\:\:\boldsymbol{{d}},\:\boldsymbol{{h}},\:{and}\:\boldsymbol{{k}}\:\left({as}\:{shown}\:{in}\:{diagram}\right. \\ $$$$\left.{above}\:\right). \\ $$$${Let}\:{AB}\:{be}\:\boldsymbol{{d}}\:{units}\:{above}\:{x}-{axes}. \\ $$$${equation}\:{of}\:{AB}\:{is}\:{then}\: \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}=\boldsymbol{{d}}\:\:\: \\ $$$${let}\:{C}\:{have}\:{coordinates}\:\left(\boldsymbol{{x}}_{{C}} \:,\:\boldsymbol{{k}}+\boldsymbol{{d}}\right) \\ $$$${As}\:{A}\:{lies}\:{on}\:{circle}\:{with}\:{radius}\:\boldsymbol{{a}}, \\ $$$$\:\:{and}\:{also}\:{on}\:{AB},\:{we}\:{have} \\ $$$$\:\:\:\:{x}_{{A}} ={x}_{{C}} −{h}\:\:\:\:{and}\:\:\:{y}_{{A}} ={d} \\ $$$$\:\:\:\:\left({x}_{{C}} −{h}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} =\:{a}^{\mathrm{2}} \:\:\:\:\:…..\left({i}\right) \\ $$$$\:{similarly}\:{for}\:{point}\:{B}\left({x}_{{C}} +{h},\:{d}\right) \\ $$$$\:\:\:\:\left({x}_{{C}} +{h}\right)^{\mathrm{2}} +{d}^{\:\mathrm{2}} ={b}^{\mathrm{2}} \:\:\:\:\:\:…..\left({ii}\right) \\ $$$${and}\:{for}\:{point}\:{C}\:\left({x}_{{C}} \:,\:{k}+{d}\right) \\ $$$$\:\:\:\:\:{x}_{{C}} ^{\mathrm{2}} \:+\left({k}+{d}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \:\:\:\:\:\:\:\:…..\left({iii}\right) \\ $$$${and}\:{finally}\:,\:{as}\:\Delta\:{is}\:{equilateral}, \\ $$$$\mathrm{tan}\:\angle{CAB}=\frac{{k}}{{h}}\:\:\: \\ $$$$\:\:\:\:{or}\:\:\:\:\:\:\frac{{k}}{{h}}\:=\mathrm{tan}\:\frac{\pi}{\mathrm{3}}\:=\sqrt{\mathrm{3}}\:\:\:….\left({iv}\right) \\ $$$$\:{solving}\:{them}\:\left({is}\:{tedious}\right),\: \\ $$$$\:…… \\ $$$$\:\:\:…… \\ $$$$\:\:\:\:\:……\:\:\:{solving}\:….. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17
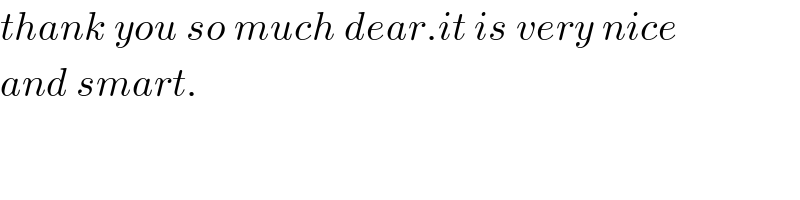
$${thank}\:{you}\:{so}\:{much}\:{dear}.{it}\:{is}\:{very}\:{nice} \\ $$$${and}\:{smart}. \\ $$
Commented by RasheedSoomro last updated on 16/Jun/17

$$\boldsymbol{\mathrm{V}}\:\boldsymbol{\mathrm{Nice}}\:\mathrm{Sir}! \\ $$$$\:^{\bullet} \mathrm{Sir},\:\mathrm{can}\:\mathrm{such}\:\mathrm{triangle}\:\mathrm{be}\:\mathrm{drawn} \\ $$$$\mathrm{using}\:\mathrm{Euclidean}\:\mathrm{tools}\left(\mathrm{straightedge}\right. \\ $$$$\left.\&\:\mathrm{compass}\right)\mathrm{only}? \\ $$$$\:^{\bullet} \mathrm{Can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{without}\:\mathrm{analytical} \\ $$$$\mathrm{approach}? \\ $$
Commented by mrW1 last updated on 17/Jun/17

$$\mathrm{Yes},\:\mathrm{such}\:\mathrm{a}\:\mathrm{triangle}\:\left(\mathrm{usually}\:\mathrm{two}\right)\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{drawn}\:\mathrm{using}\:\mathrm{E}'\:\mathrm{tools}\:\mathrm{only}.\:\mathrm{With} \\ $$$$\mathrm{analytical}\:\mathrm{approach}\:\mathrm{a}\:\mathrm{cubic}\:\mathrm{equation} \\ $$$$\mathrm{is}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}. \\ $$
