Question Number 159999 by Tawa11 last updated on 23/Nov/21

Answered by Kunal12588 last updated on 23/Nov/21
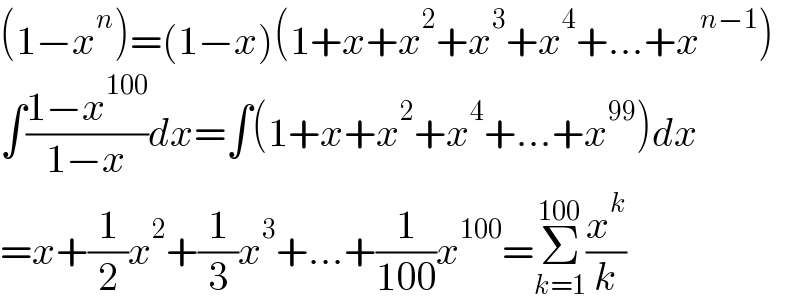
$$\left(\mathrm{1}−{x}^{{n}} \right)=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +…+{x}^{{n}−\mathrm{1}} \right) \\ $$$$\int\frac{\mathrm{1}−{x}^{\mathrm{100}} }{\mathrm{1}−{x}}{dx}=\int\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +…+{x}^{\mathrm{99}} \right){dx} \\ $$$$={x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +…+\frac{\mathrm{1}}{\mathrm{100}}{x}^{\mathrm{100}} =\underset{{k}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{{x}^{{k}} }{{k}} \\ $$
Commented by Tawa11 last updated on 24/Nov/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
