Menu Close

Question-160014

Tinku Tara 0 Comments
Pin




Question Number 160014 by mr W last updated on 23/Nov/21
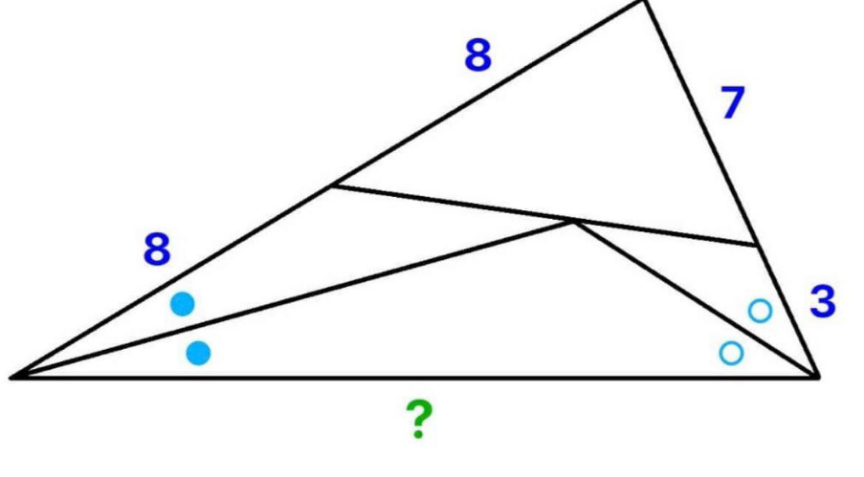
Commented by mr W last updated on 23/Nov/21
Q158675
$${Q}\mathrm{158675} \\ $$
Commented by mr W last updated on 24/Nov/21
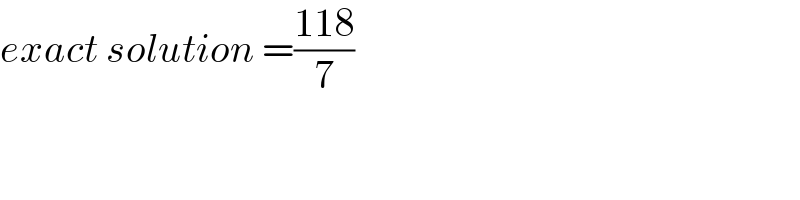
exact solution =((118)/7)
$${exact}\:{solution}\:=\frac{\mathrm{118}}{\mathrm{7}} \\ $$
Answered by mr W last updated on 23/Nov/21
Commented by mr W last updated on 24/Nov/21
((BF)/(BA))=((FG)/(GA))=((FC)/(CA)) ((BF)/(16))=((FG)/p)=((FC)/(10))=k, say ⇒BF=16k, FC=10k, FG=kp ((16^2 k^2 +(1+k)^2 p^2 −16^2 )/(2×16k×(1+k)p))=−((10^2 k^2 +(1+k)^2 p^2 −10^2 )/(2×10k×(1+k)p)) (((1+k)^2 p^2 −16^2 (1−k^2 ))/8)=−(((1+k)^2 p^2 −10^2 (1−k^2 ))/5) (((1+k)p^2 −16^2 (1−k))/8)=−(((1+k)p^2 −10^2 (1−k))/5) 5(1+k)p^2 −5×16^2 (1−k)+8(1+k)p^2 −8×10^2 (1−k)=0 13(1+k)p^2 =(5×16^2 +8×10^2 )(1−k) ⇒p^2 =((160(1−k))/(1+k)) ((8^2 +p^2 −s^2 )/(2×8×p))=((16^2 +(1+k)^2 p^2 −16^2 k^2 )/(2×16×(1+k)p)) 8^2 +p^2 −s^2 =(((1+k)p^2 +16^2 (1−k))/2) s^2 =(((1−k)p^2 )/2)+64(2k−1) s^2 =((80(1−k)^2 )/(1+k))+64(2k−1) ⇒s=4(√((13k^2 −6k+1)/(1+k))) ...(i) ((7^2 +p^2 −t^2 )/(2×7×p))=((10^2 +(1+k)^2 p^2 −10^2 k^2 )/(2×10×(1+k)p)) ((7^2 +p^2 −t^2 )/7)=(((1+k)p^2 +10^2 (1−k))/(10)) t^2 =(((3−7k)p^2 )/(10))+70k−21 t^2 =((16(3−7k)(1−k))/(1+k))+70k−21 ⇒t=(√((182k^2 −111k+27)/(1+k))) ...(ii) ((8^2 +7^2 −(s+t)^2 )/(2×8×7))=((16^2 +10^2 −26^2 k^2 )/(2×16×10)) ((113−(s+t)^2 )/7)=((89−169k^2 )/5)e 113×5−5(s+t)^2 =7×89−7×169k^2 ⇒1183k^2 −5(s+t)^2 =58 ...(iii) inserting (i) and (ii) into (iii), we get k≈0.64835165 and k=1 (rejected) ⇒?=BC=26k≈16.857143 ==================== exact solution: 5(s^2 +t^2 +2st)=1183k^2 −58 5(390k^2 −207k+43)+40(√((13k^2 −6k+1)(182k^2 −111k+27)))=(1183k^2 −58)(1+k) 40(√((13k^2 −6k+1)(182k^2 −111k+27)))=1183k^3 −767k^2 +977k−273 1600(13k^2 −6k+1)(182k^2 −111k+27)=(1183k^3 −767k^2 +977k−273)^2 (k−1)(k+1)(13k−3)(13k+3)(91k−59)^2 =0 k=±1 (rejected, since k<((16+10)/(26))=1) k=±(3/(13)) (rejected, since k>((16−10)/(26))=(3/(13))) k=((59)/(91)) ✓ ⇒?=BC=26k=((26×59)/(91))=((118)/7)≈16.857
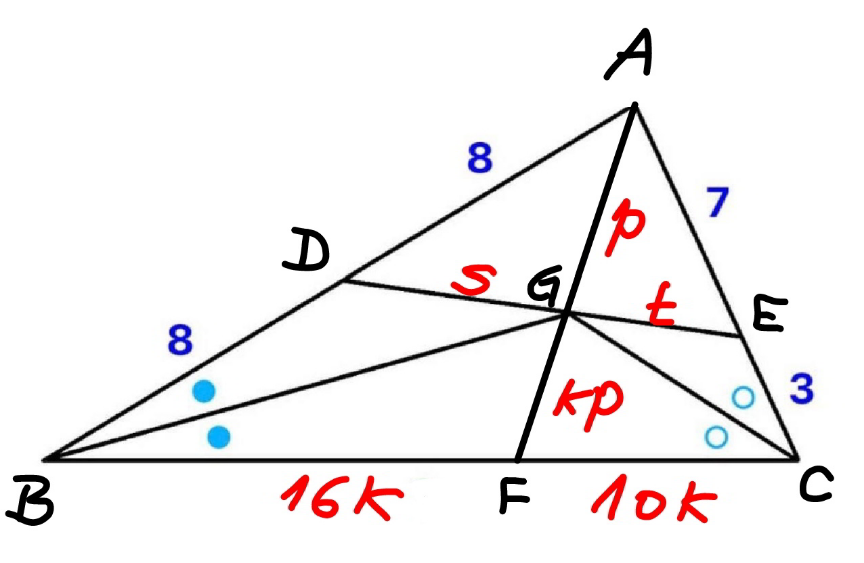
$$\frac{{BF}}{{BA}}=\frac{{FG}}{{GA}}=\frac{{FC}}{{CA}} \\ $$$$\frac{{BF}}{\mathrm{16}}=\frac{{FG}}{{p}}=\frac{{FC}}{\mathrm{10}}={k},\:{say} \\ $$$$\Rightarrow{BF}=\mathrm{16}{k},\:{FC}=\mathrm{10}{k},\:{FG}={kp} \\ $$$$\frac{\mathrm{16}^{\mathrm{2}} {k}^{\mathrm{2}} +\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} }{\mathrm{2}×\mathrm{16}{k}×\left(\mathrm{1}+{k}\right){p}}=−\frac{\mathrm{10}^{\mathrm{2}} {k}^{\mathrm{2}} +\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }{\mathrm{2}×\mathrm{10}{k}×\left(\mathrm{1}+{k}\right){p}} \\ $$$$\frac{\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} \left(\mathrm{1}−{k}^{\mathrm{2}} \right)}{\mathrm{8}}=−\frac{\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} \left(\mathrm{1}−{k}^{\mathrm{2}} \right)}{\mathrm{5}} \\ $$$$\frac{\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)}{\mathrm{8}}=−\frac{\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)}{\mathrm{5}} \\ $$$$\mathrm{5}\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} −\mathrm{5}×\mathrm{16}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)+\mathrm{8}\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} −\mathrm{8}×\mathrm{10}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)=\mathrm{0} \\ $$$$\mathrm{13}\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} =\left(\mathrm{5}×\mathrm{16}^{\mathrm{2}} +\mathrm{8}×\mathrm{10}^{\mathrm{2}} \right)\left(\mathrm{1}−{k}\right) \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\mathrm{160}\left(\mathrm{1}−{k}\right)}{\mathrm{1}+{k}} \\ $$$$\frac{\mathrm{8}^{\mathrm{2}} +{p}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×{p}}=\frac{\mathrm{16}^{\mathrm{2}} +\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} {k}^{\mathrm{2}} }{\mathrm{2}×\mathrm{16}×\left(\mathrm{1}+{k}\right){p}} \\ $$$$\mathrm{8}^{\mathrm{2}} +{p}^{\mathrm{2}} −{s}^{\mathrm{2}} =\frac{\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} +\mathrm{16}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)}{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\frac{\left(\mathrm{1}−{k}\right){p}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{64}\left(\mathrm{2}{k}−\mathrm{1}\right) \\ $$$${s}^{\mathrm{2}} =\frac{\mathrm{80}\left(\mathrm{1}−{k}\right)^{\mathrm{2}} }{\mathrm{1}+{k}}+\mathrm{64}\left(\mathrm{2}{k}−\mathrm{1}\right) \\ $$$$\Rightarrow{s}=\mathrm{4}\sqrt{\frac{\mathrm{13}{k}^{\mathrm{2}} −\mathrm{6}{k}+\mathrm{1}}{\mathrm{1}+{k}}}\:\:…\left({i}\right) \\ $$$$\frac{\mathrm{7}^{\mathrm{2}} +{p}^{\mathrm{2}} −{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{p}}=\frac{\mathrm{10}^{\mathrm{2}} +\left(\mathrm{1}+{k}\right)^{\mathrm{2}} {p}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} {k}^{\mathrm{2}} }{\mathrm{2}×\mathrm{10}×\left(\mathrm{1}+{k}\right){p}} \\ $$$$\frac{\mathrm{7}^{\mathrm{2}} +{p}^{\mathrm{2}} −{t}^{\mathrm{2}} }{\mathrm{7}}=\frac{\left(\mathrm{1}+{k}\right){p}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} \left(\mathrm{1}−{k}\right)}{\mathrm{10}} \\ $$$${t}^{\mathrm{2}} =\frac{\left(\mathrm{3}−\mathrm{7}{k}\right){p}^{\mathrm{2}} }{\mathrm{10}}+\mathrm{70}{k}−\mathrm{21} \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{16}\left(\mathrm{3}−\mathrm{7}{k}\right)\left(\mathrm{1}−{k}\right)}{\mathrm{1}+{k}}+\mathrm{70}{k}−\mathrm{21} \\ $$$$\Rightarrow{t}=\sqrt{\frac{\mathrm{182}{k}^{\mathrm{2}} −\mathrm{111}{k}+\mathrm{27}}{\mathrm{1}+{k}}}\:\:\:…\left({ii}\right) \\ $$$$\frac{\mathrm{8}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\left({s}+{t}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×\mathrm{7}}=\frac{\mathrm{16}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{26}^{\mathrm{2}} {k}^{\mathrm{2}} }{\mathrm{2}×\mathrm{16}×\mathrm{10}} \\ $$$$\frac{\mathrm{113}−\left({s}+{t}\right)^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{89}−\mathrm{169}{k}^{\mathrm{2}} }{\mathrm{5}}{e} \\ $$$$\mathrm{113}×\mathrm{5}−\mathrm{5}\left({s}+{t}\right)^{\mathrm{2}} =\mathrm{7}×\mathrm{89}−\mathrm{7}×\mathrm{169}{k}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1183}{k}^{\mathrm{2}} −\mathrm{5}\left({s}+{t}\right)^{\mathrm{2}} =\mathrm{58}\:\:\:…\left({iii}\right) \\ $$$${inserting}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{into}\:\left({iii}\right),\:{we}\:{get} \\ $$$${k}\approx\mathrm{0}.\mathrm{64835165}\:{and}\:{k}=\mathrm{1}\:\left({rejected}\right) \\ $$$$\Rightarrow?={BC}=\mathrm{26}{k}\approx\mathrm{16}.\mathrm{857143} \\ $$$$==================== \\ $$$${exact}\:{solution}: \\ $$$$\mathrm{5}\left({s}^{\mathrm{2}} +{t}^{\mathrm{2}} +\mathrm{2}{st}\right)=\mathrm{1183}{k}^{\mathrm{2}} −\mathrm{58} \\ $$$$\mathrm{5}\left(\mathrm{390}{k}^{\mathrm{2}} −\mathrm{207}{k}+\mathrm{43}\right)+\mathrm{40}\sqrt{\left(\mathrm{13}{k}^{\mathrm{2}} −\mathrm{6}{k}+\mathrm{1}\right)\left(\mathrm{182}{k}^{\mathrm{2}} −\mathrm{111}{k}+\mathrm{27}\right)}=\left(\mathrm{1183}{k}^{\mathrm{2}} −\mathrm{58}\right)\left(\mathrm{1}+{k}\right) \\ $$$$\mathrm{40}\sqrt{\left(\mathrm{13}{k}^{\mathrm{2}} −\mathrm{6}{k}+\mathrm{1}\right)\left(\mathrm{182}{k}^{\mathrm{2}} −\mathrm{111}{k}+\mathrm{27}\right)}=\mathrm{1183}{k}^{\mathrm{3}} −\mathrm{767}{k}^{\mathrm{2}} +\mathrm{977}{k}−\mathrm{273} \\ $$$$\mathrm{1600}\left(\mathrm{13}{k}^{\mathrm{2}} −\mathrm{6}{k}+\mathrm{1}\right)\left(\mathrm{182}{k}^{\mathrm{2}} −\mathrm{111}{k}+\mathrm{27}\right)=\left(\mathrm{1183}{k}^{\mathrm{3}} −\mathrm{767}{k}^{\mathrm{2}} +\mathrm{977}{k}−\mathrm{273}\right)^{\mathrm{2}} \\ $$$$\left({k}−\mathrm{1}\right)\left({k}+\mathrm{1}\right)\left(\mathrm{13}{k}−\mathrm{3}\right)\left(\mathrm{13}{k}+\mathrm{3}\right)\left(\mathrm{91}{k}−\mathrm{59}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${k}=\pm\mathrm{1}\:\left({rejected},\:{since}\:{k}<\frac{\mathrm{16}+\mathrm{10}}{\mathrm{26}}=\mathrm{1}\right) \\ $$$${k}=\pm\frac{\mathrm{3}}{\mathrm{13}}\:\left({rejected},\:{since}\:{k}>\frac{\mathrm{16}−\mathrm{10}}{\mathrm{26}}=\frac{\mathrm{3}}{\mathrm{13}}\right) \\ $$$${k}=\frac{\mathrm{59}}{\mathrm{91}}\:\checkmark \\ $$$$\Rightarrow?={BC}=\mathrm{26}{k}=\frac{\mathrm{26}×\mathrm{59}}{\mathrm{91}}=\frac{\mathrm{118}}{\mathrm{7}}\approx\mathrm{16}.\mathrm{857} \\ $$
Commented by Tawa11 last updated on 23/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 23/Nov/21
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *